Discovering a nontriviality of the ε-δ definition, in a math way
Published:
This is a record of a talk that I made in the UChicago Math dept. Pedagogy seminar, in 2022-02-23.
Hurdles to understand the Standard Definition
A student of calculus who first gets introduced to the precise definition of the limit $\lim_{x\to c}f(x)=L$, should overcome some mental challenges to understand the following definition.
($\epsilon$-$\delta$) For all $\epsilon>0$, there exists $\delta>0$ in which, $0<\vert x-c\vert<\delta$ implies $\vert f(x)-L\vert<\epsilon$.
There are several layers of hurdles to understanding this:
- To understand why we use a lot of absolute values $\vert\cdot\vert$; especially, understanding that the concept of distance is intervening.
- To understand the logical quantifiers and connectives, like “for all” “there exists” or “implies”.
- To make sense of why we have a particular order $\forall\epsilon\exists\delta$ in the definition.
Practically, the first two lines are already some challenges for a typical freshman calculus student. Especially for those instructors who cannot pay for more than two weeks, focusing on the first two (i.e., to understand the words per se) would be challenging enough for the students.
The third line seems to be an interest for a limited number of people (as my experience as a student and as an instructor tells). But ironically, this holds all the connection from the infamous “intuitive” definition of limits to the standard definition ($\epsilon$-$\delta$).
An Infamous ‘Definition’
The infamous “intuitive” definition of the limit $\lim_{x\to c}f(x)=L$ reads as follows.
(?) As $x$ approaches to $c$, the value $f(x)$ approaches to $L$.
I have labeled this as (?), to avoid giving any meaningful name for this ‘definition.’ Nonetheless, we have some contrast between the definition (?) and the standard definition ($\epsilon$-$\delta$) above, in the following way.
- Definition (?) starts from a control on the domain and asserts its result on the range.
- Definition ($\epsilon$-$\delta$) starts with $\epsilon>0$ that controls the range, then gives the variable $\delta>0$ that controls the domain.
So apparently, the order of domain and range controls seems to be inverted between (?) and ($\epsilon$-$\delta$). Understanding this is the main key to hurdle 3 (“Why the order $\forall\epsilon\exists\delta$?”).
It is not surprising to believe that every instructor teaching calculus has a rationale to answer why the order makes sense. (Say, by some cases where ‘weird’ quantifying does not make sense; by some good pictures depicting why the standard choice should be the case, etc.)
As one of such rationals, I state my rationale as follows.
Claim. The order $\forall\epsilon\exists\delta$ is coming from the following inputs.
- Translating the ‘definition’ (?) into infinitesimals.
- By which we mean by ‘proving something with infinitesimals.’
- The compactness principle in mathematical logic.
Infinitesimal Definition
For brievity, I assume $c=L=0$ from now on. That is, I only focus on the case $\lim_{x\to 0}f(x)=0$.
If one admits to using infinitesimals, one can translate the ‘definition’ (?) as follows.
(INF) If $x\neq 0$ is an infinitesimal, then so is $f(x)$.
I believe that this paraphrase of (?) is more coherent to implicit understandings of the limits, but was later banned in 19C. A summarized story, following Mormann & Katz 2013, goes as follows.
- People started using infinitesimals, despite their ill-logical nature.
- In late 19C, Cantor, Dedekind, and Weierstrass’ ‘rigorization project’ succeeded to ban the infinitesimals from our calculus textbooks.
- In 1961, A. Robinson succeeded in a set-theoretical ontology of defining infinitesimals; a calculus text by Keisler 1971 was then published as the first text in ‘calculus with infinitesimals.’
Infinitesimal Definition taught in classes
Interestingly, the story keeps on even for 21C. A pedagogical ‘experiment’ reported in Katz & Polev 2017 gives some interesting data:
The authors asked students to prove \(\lim_{x\to 2}(x+5)=7,\) and students attempted (INF) and ($\epsilon$-$\delta$) in their solutions:
- For (INF), 98% attempted this. 85% succeeded among those attempted.
- For ($\epsilon$-$\delta$), 71% attempted this. 20% succeeded among those attempted.
(To be fair, the course was designed to give an extensive practice on the ($\epsilon$-$\delta$) definition.)
Student poll results, on thoughts regarding how each definition was helping for understanding:
| Continuity | Convergent Sequences | |||
| All | Knows def'n | All | Knows def'n | |
| ($\epsilon$-$\delta$) | 10% | 9% | 21% | 24% |
| (INF) | 69% | 75% | 74% | 80% |
(See Katz & Polev 2017, sec. 3 for more data.)
A couple of interesting conclusions may be drawn from this:
- We still long for infinitesimals (at least for first learners).
- Sequences are surprisingly well-understood, even with $\epsilon$-$\delta$ definitions.
- (from Katz & Polev 2017) Once the students understand the basic concepts via their intuitive (INF) formulations, they are able to relate more easily to the ($\epsilon$-$\delta$) paraphrases of the definition.
Foundational Details of Infinitesimals
Although the infinitesimal definition is elegant and easy to be understood, things happening under the rug is quite complicated. Even for Keisler 1971, the way how infinitesimals are founded in the main text is based on the property it enjoys:
We say a number $x$ in which $-a<x<a$ holds for all positive real $a>0$, as infinitesimals.
The text then develops various calculus notions out of this.
The precise construction is introduced in the epilogue of the text. In analogy with the construction of real numbers (as equivalence classes of Cauchy sequences), the field of hyperreal numbers is defined using the notion of ‘ultraproduct equivalence.’
There, any discussions on the existence or the variety of such equivalence were skipped. I view this as a reasonable choice, however. Even for those who are interested in such issues, as far as I know, the minimal background to understand the precise construction of hyperreal numbers is the Stone-Čech compactification. This topic is one of the high-end topics in undergraduate point-set topology courses. A corollary is that digging into the most basic foundation (of infinitesimals) is infeasible for calculus students.
Compactness, Equivalence
We say a number $x$ is an infinitesimal if we have $-a<x<a$ for all positive real $a>0$. On one hand, this may be viewed as a hyperreal number. But logically speaking, we may view this as an object $x$ in which the formulas $-a<x<a$ are always interpreted true, whenever $a$ is a positive real number.1
Applying this logical viewpoint, one can translate the definition (INF) as follows.
(INF-logic) From the assumptions \(\{0<\vert x\vert<a : a>0\}\), one can prove that $\vert f(x)\vert<\epsilon$, no matter what $\epsilon>0$ is.
Equivalently,
(INF-logic) For all $\epsilon>0$, the assumptions \(\{0<\vert x\vert<a : a>0\}\) can prove that $\vert f(x)\vert<\epsilon$.
(So this already clears $\forall\epsilon$ start. But we are still left to quantify $\delta$.)
Now I state a principle in mathematical logic: the compactness.
(A version of) Compactness in Math. Logic. Let $\Gamma$ be a set of assumptions, and let $\Gamma\vdash\phi$ (i.e., $\Gamma$ can prove a statement $\phi$). Then there is a finite subset $\Gamma’\subset\Gamma$ in which $\Gamma’\vdash\phi$.
The proof is surprisingly easy for this one:2
(Proof) If we write down a proof of $\phi$, then the lines we use are finite. In particular, the lines that introduce assumptions from $\Gamma$ are finite. Putting $\Gamma’$ the set of lines that introduces assumptions, we see that only $\Gamma’$ suffices to get $\phi$.
If this proof is applied for (INF-logic), then we see that only some hypotheses $0<\vert x\vert<\delta_1$, …, $0<\vert x\vert <\delta_k$ are used to prove $\vert f(x)\vert<\epsilon$. This is analogous to the following solution of a $\epsilon$-$\delta$ limit proof exercise:
(To prove $\lim_{x\to 2}x^2=4$, fix $\epsilon>0$.) Let $0<\vert x-2\vert<1$ and $0<\vert x-2\vert<\epsilon/5$. Then by […omitted…], we can infer $\vert x^2-4\vert<\epsilon$.
Anyways, setting $\delta=\min(\delta_1,\cdots,\delta_k)$, we finally translate (INF-logic) into the following.
For all $\epsilon>0$, there is an assumption $0<\vert x\vert<\delta$ that can prove $\vert f(x)\vert<\epsilon$.
By this, we can prove that (INF) is equivalent to ($\epsilon$-$\delta$) (independent of how infinitesimals are implemented!). The cost was some principles in mathematical logic.
This also gives a ‘math’ proof of why $\forall\epsilon\exists\delta$ order is compulsory. (Personal history: this took me around a decade and a half to figure this out.)
1. The ultraproduct definition of hyperreal numbers is, as far as I know, a way to implement this viewpoint.↩
2. There are other versions of compactness in mathematical logic, that require some involved proofs.↩
Detouring Definitions
As usual, we let $c=L=0$, i.e., get interested in $\lim_{x\to 0}f(x)=0$.
We have seen that the ‘infinitesimal’ definition (INF) is equivalent to the standard definition ($\epsilon$-$\delta$) by mathematical logic. However, we have also seen that (INF) is closer to our intuition of limit, in various ways. For instance, the domain-range logical order is well-preserved in (INF).
Thus I introduce some paraphrases of (INF), in search of a more intuitive, yet precise definition of limits.
Remark
- It should be noted that each definition below has its limits to be a pedagogical replacement of the ($\epsilon$-$\delta$) definition.
- For instance, for the (Sequence) definition below, it is not quite clear how students perceive the quantification “for all sequences.” The definition is more suitable to disprove some facts on limits. To prove a limit fact with this definition, we often require a task equivalent to doing some $\epsilon$-$\delta$ proofs. Such a workload is easily overlooked by the definition alone.
Sequence Definition
A standard way to simulate infinitesimals is to use sequences. (Also, it is coherent with the ultraproduct construction of hyperreals.) Thus if $(a_n)$ is a sequence of nonzero numbers converging to 0, we can simulate an infinitesimal by this sequence. So if (INF) is valid, then $(f(a_n))$ is another sequence that simulates infinitesimals, i.e., converges to 0.
(Sequence) If $(a_n)$ is a sequence, $a_n\neq 0$ for all $n$, that converges to 0, then the sequence $(f(a_n))$ also converges to 0.
Indeed, this is formatted as, “a control on domain determines feature on the range.” Furthermore, this definition is written in terms of convergent sequences; recall that convergent sequences are more easily understood by the first readers.
Squeeze Perspective
Another way to say ‘$f(x)$ is an infinitesimal’ (given $x$ infintiesimal) is to say that, there are two infinitesimals $\epsilon_1,\epsilon_2$ in which $\epsilon_1<f(x)<\epsilon_2$. Applying this notion, we get
(Squeeze) If $(a_n)\to 0$, $a_n\neq 0$ for all $n$, then there are sequences $(\epsilon^1_n)\nearrow 0$ and $(\epsilon^2_n)\searrow 0$ that $\epsilon^1_n<f(a_n)<\epsilon^2_n$ holds.
This itself is not looking that practical. However, this is more like an abstraction of what students do for their first limit proofs:
- Play with $f(x)-L$, so that one can obtain a Lipschitz bound $\vert f(x)-L\vert\leq M\vert x-c\vert$, whenever $0<\vert x-c\vert<a$.
- Use that Lipschitz bound to suggest $\delta=\min(a,\epsilon/M)$.
The squeezing sequences \((\epsilon^1_\bullet)\) and \((\epsilon^2_\bullet)\) are hence simulators of Lipschitz estimates (or other kinds of estimates). The use of sequence is, really, just a way to abstract various estimates that contributes limit proofs.
Limsup and liminf
For (Squeeze), we have a systematic choice of the bounds \((\epsilon^1_\bullet)\) and \((\epsilon^2_\bullet)\):
\[\epsilon^1_k := \inf_{n\geq k}f(a_n), \\ \epsilon^2_k := \sup_{n\geq k}f(a_n).\]That is, we simply think of $\limsup f(a_n)$ and $\liminf f(a_n)$. Furthermore, there is no reason to not generalize this for non-sequence versions. Call,
\[\liminf_{x\to c}f(x) = \sup_{\delta>0}\inf_{x\colon 0<|x-c|<\delta}f(x), \\ \limsup_{x\to c}f(x) = \inf_{\delta>0}\sup_{x\colon 0<|x-c|<\delta}f(x).\]Then we say $\lim_{x\to c}f(x)=L$ if
(limsup-liminf) we have $\limsup_{x\to c}f(x)=\liminf_{x\to c}f(x)=L$.
An easy drawback of this definition is, that we necessarily introduce harder topics of suprema and infima. A benefit of this definition is, that it is much easier for this definition to come up with a picture.
For instance, one can sketch the limit of sequences by thinking of “sup and inf hammers that approach together.”
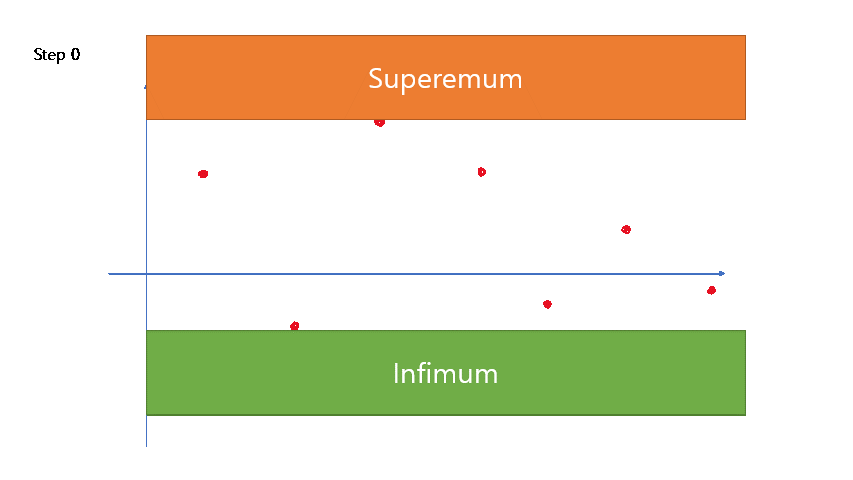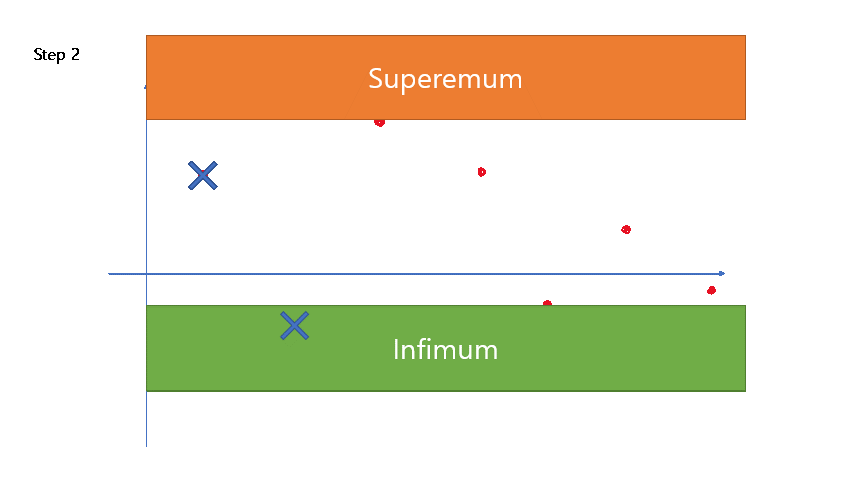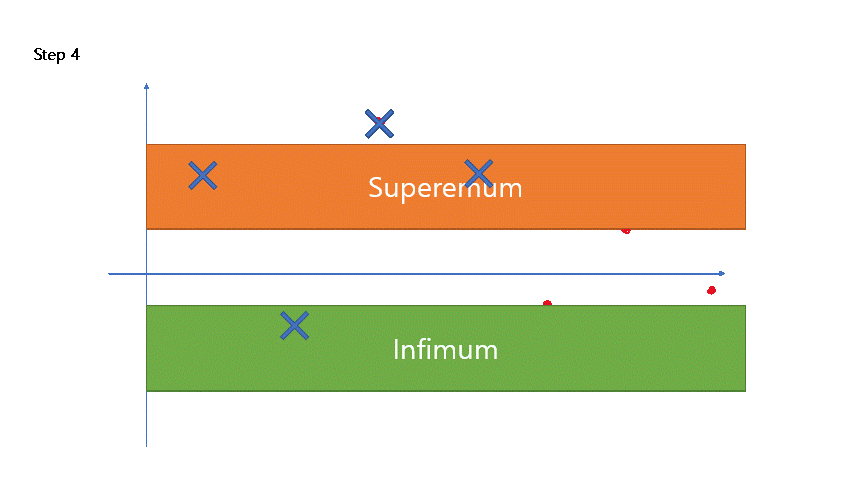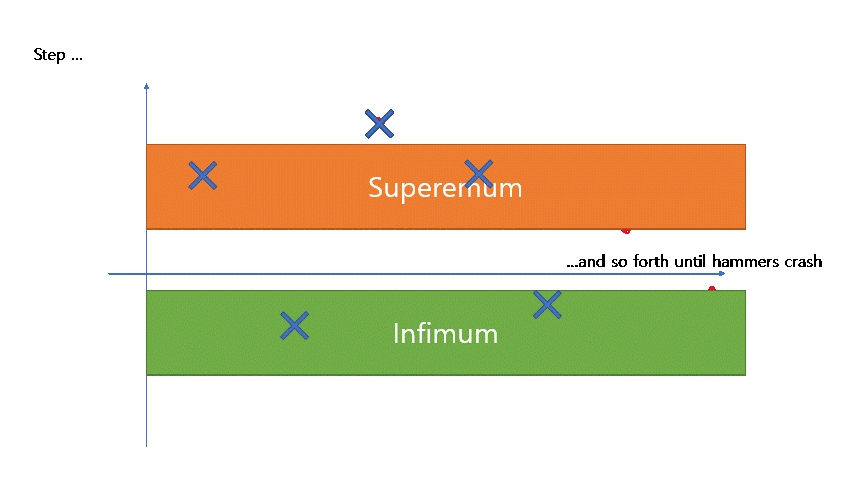
One can easily add a sense of a video game (say, a game character crashing each sequence term, and hammers crashing up/down because the sequence terms holding them is no longer there) for this picture.
An analogue for the limit $\lim_{x\to c}f(x)=L$ may also be established. To do so, we ‘trim’ the parts of the graph near $x\approx c$, and trace where sup and inf hammers go. (Again, contextualizing this with video games will help this picture more concentrative.)
Post-remarks
- The motivation of the post was my success in introducing $\limsup a_n$ and $\liminf a_n$ of bounded sequences in a calculus course. Not only it was good for standard limit exercises, but the notion was very useful to explain why the alternating series test works. For an alternating series $\sum(-1)^na_n$ with $a_n\geq 0$ decreasing, the gap between sup and inf hammers is precisely $a_n$. (Thus $a_n\to 0$ iff convergent.)
- Although students may find the $\epsilon$-$\delta$ definition not very motivating in general, it can also be some interesting math topic in some contexts. Specifically, the sequence analogue of the definition (the ‘$\epsilon$-$K$ definition’) does get interesting with the following points.3
- The definition is especially interesting if the sequence $a_n$ has a relatively simple form, e.g. $1/n^p$, $e^{-\alpha n}$, $\ln n$, …
- Using the definition is also interesting. For instance, it is not hard to show that $\ln n<n^{0.5}$ for $n>K$, $K=K(1)$ an integer, by combining $\displaystyle\lim_{n\to\infty}\frac{\ln n}{n^{0.5}}=0$ and the $\epsilon$-$K$ definition.
- The above points seem to be hard to reproduce when one plays with the limits of functions. Especially when the majority of examples are only dependent on Lipschitz bounds.
- Applying (limsup-liminf) definition does remind us what kind of mistakes are prone for students. For instance, to prove $\lim_{x\to 2}x^2=4$ using the (limsup-liminf) definition, one note that
This reminds us that, some attempts to prove $\lim_{x\to 2}x^2=4$ (esp. those not used to make appropriate bounds) are playing with terms that look like the above. The (limsup-liminf) definition may help us to guide these attempts into a context that makes mathematically a better sense.
- To prove some limit theorems, introducing ($\epsilon$-$\delta$) definition seems inevitable. One of the most fundamental fact, $f(\lim g(x))=\lim f(g(x))$ when $f$ is continuous, is not very promising if one starts with, say, (limsup-liminf) definition.
3. It should be noted that the environment for testing these points, was the final course of the calculus sequence at UChicago. That is, students were motivated and skilled enough to trace what happens for each point.↩
Appendix: Topological compactness
Another way to implement infinitesimals is to think of the Stone–Čech compactification $\beta\mathbb{R}$ of the discrete space $\mathbb{R}$. The space $\beta\mathbb{R}$ consists of ultrafilters in the set $\mathbb{R}$, and infinitesimals are ultrafilters $\in\beta\mathbb{R}$ that contain the sets of the form \(\{x : \vert x\vert<a\}\).
The benefit of $\beta\mathbb{R}$ is that, any set function $\mathbb{R}\to\mathbb{R}$ extends to a continuous map $\beta\mathbb{R}\to\beta\mathbb{R}$. Thus any set of the form \(\{x\in\beta\mathbb{R} : \vert f(x)\vert<\epsilon\}\) is actually open in $\beta\mathbb{R}$.
Denote the sets \(K_m = \{x\in\beta\mathbb{R}:0<\vert x\vert<1/m\}\) and \(U_n=\{x\in\beta\mathbb{R}:\vert f(x)\vert<1/n\}\). One can then show that $K_m$ and $U_n$ are clopen subsets of $\beta\mathbb{R}$. Furthermore, the (INF) definition of $\lim_{x\to 0}f(x)=0$ translates to
(INF-topo) $\bigcap_{m=1}^\infty K_m\subset\bigcap_{n=1}^\infty U_n$.
This immediately translates to $\bigcap_{m=1}^\infty K_m\subset U_n$, for all $n$. Equivalently, the family \(\{U_n\}\cup\{\complement K_m\}_{m=1}^\infty\) of open subsets of $\beta\mathbb{R}$ form an open cover. (Here, $\complement X:=\beta\mathbb{R}\setminus X$.) By compactness of $\beta\mathbb{R}$, we pick up a finite subcover $U_n,\complement K_{m_1},\cdots,\complement K_{m_k}$. But since $\left(K_m\right)_{m=1}^\infty$ is a decreasing sequence, putting $m=\max(m_1,\cdots,m_k)$ we see that $U_n$ and $\complement K_m$ covers $\beta\mathbb{R}$, i.e., $K_m\subset U_n$ holds. In short:
(INF-topo) $\Leftrightarrow$ $(\forall n)(\bigcap_{m=1}^\infty K_m\subset U_n)$ $\Leftrightarrow$ $(\forall n)(\exists m)(K_m\subset U_n)$,
and the last equivalence is where compactness is involved. There I suggest a slogan for $\forall\epsilon\exists\delta$ order:
The order $\forall\epsilon\exists\delta$ in the ($\epsilon$-$\delta$) definition is a result of compactness.
Update Log
- 220324: Created
- 220324: Typo/elaboration, as suggested from J. Jeon
- 220528-9: Grammar fixes; polishing sentences