「호몰로지」 용어에 대한 일고(一考)

대한수학회 수학용어집에 따르면, homology, cohomology는 각각 음값을 그대로 쓴 ‘호몰로지’ ‘코호몰로지’라 번역하는 것이 표준이다. 다만, 보다 원어의 의미를 잘 생각해 보고자, 이 용어가 어떤 맥락에서 도입됐는지 등에 대해 알아 본 내용을 담아 보았다.

「호몰로지」 용어의 역사

C. A. Weibel의 호몰로지 대수의 역사 중 3페이지에 따르면, 푸앵카레의 1895년 논문 Analysis Situs에서 제시된 용어가 용어 자체의 시작점으로 보인다.

(Weibel의 글에서) 푸앵카레 이전의 내용으로, 리만과 (B. Riemann) 베티의 (E. Betti) 저작을 언급하고는 있다. 그러나 리만과 베티의 연구에서 호몰로지의 개념은 등장하지만, 이것을 ‘호몰로지’라고 굳이 명명한 것은 푸앵카레의 업적으로 보인다. 따라서 위 소개문에서 언급한 Analysis Situs 에서, 보다 역사적인 맥락을 기대할 수 있겠다.

Analysis Situs 내에서

푸앵카레가 처음 ‘호몰로지’ 용어를 언급한 Analysis Situs의 원문 및 J. Stillwell의 번역 모두 비교적 쉽게 확인할 수 있는 문헌이다. (Wikipedia 2차인용.) 아래에 불어 원문을 게재한다.

Sec. 5. Homologies

Considérons une variété $V$ à $p$ dimensions; soit maintenant $W$ une variété à $q$ dimensions ($q\leq p$) faisant partie de $V$. Supposons que la frontière complète de $W$ se compose de $\lambda$ variétés continues à $q-1$ dimensions

\[v_1, v_2, \ldots, v_\lambda.\]

Nous exprimerons ce fait par la notation

\[v_1+v_2+\ldots+v_\lambda\sim 0.\]

Plus généralement la notation

\[k_1v_1 + k_2v_2 \sim k_3v_3 + k_4v_4,\]

où les $k$ sont des entiers et les $v$ des variétés à $q-1$ dimensions, signifiera qu’il existe une variété $W$ à $q$ dimensions faisant partie de $V$ et dont la frontière complète se composera de \(k_1\) variétés peu différentes de \(v_1\), de \(k_2\) variétés peu différentes de \(v_2\), de \(k_3\) variétés peu différentes de la variété opposée à \(v_3\) et de \(k_4\) variétés peu différentes de la variété opposée à \(v_4\).

Les relations de cette forme pourront s’appeler des homologies.

(하략)

J. Stillwell의 영역을 참고하여 한역한 결과는 아래와 같다.

Sec. 5. 호몰로지

$p$차원 다양체 $V$을 생각하자. 또 $W$를 $q$차원 ($q\leq p$) 다양체로 두되, $V$의 일부로 주어졌다 하자. 여기에 $W$의 경계가 $\lambda$개의 $(q-1)$차원 다양체

\[v_1, v_2, \ldots, v_\lambda.\]

로 이루어졌다고 하자. 이 상황을 다음 기호로 표기한다.

\[v_1+v_2+\ldots+v_\lambda\sim 0.\]

보다 일반적으로는 다음 기호를 도입한다.

\[k_1v_1 + k_2v_2 \sim k_3v_3 + k_4v_4,\]

단 여기서 $k$는 정수, $v$는 $(q-1)$차원 다양체를 나타낸다. 이 때 어떤 $q$차원 다양체 $W$가 $V$의 부분으로서 있어, 그 경계가 \(k_1\)개의 \(v_1\)과 닮은 다양체, \(k_2\)개의 \(v_2\)와 닮은 다양체, \(k_3\)개의 \(v_3\)과 닮았으나 반대 방향을 가진 다양체, \(k_4\)개의 \(v_4\)와 닮았으나 반대 방향을 가진 다양체로 이루어졌다는 것이 위 기호의 정의이다.

이와 같은 관계를 호몰로지라 부를 것이다.

(하략)

이 이전의 Analysis Situs 의 내용은 다양체의 정의, 위상동형사상의 뜻, 다양체의 방향성 등 기초적(이면서 푸앵카레 당대의 다양체에 대한 이해를 담은)인 내용으로 이뤄져 있어, 이 절 외에 “왜 호몰로지라 불렀는가?”에 대한 단서는 얻기 힘들 것으로 보인다.

역사적으로는, 19세기 말 당시에는 이미 호몰로지라는 말 자체가 상동성(homology, 생물학 용어) 등의 뜻으로 쓰이고 있었다. (그리고 진화론 등 이와 관련한 과학이 큰 주목을 받을 즈음이기도 하다.) 때문에 ‘호몰로지’ 용어의 도입은 그 앞에서 언급한 내용으로부터 자연스럽게 연결되어 등장한 말이었면 그랬지, 완전히 없던 곳에서 창조된 용어는 아닌 셈이다.

‘호몰로지’ 용어 도입에 앞선 내용은, 호몰로지가 어떤 다양체의 경계를 기존에 알고 있던 다양체와 닮은 모양으로 써내려간다는 뜻임을 명시하고 있다. 이에 사견으로, 다양한 생물끼리 상동기관을 공유하듯, 주어진 다양체의 목록이 마치 다른 다양체의 경계에서 그 “상동 꼴”을 가지고 있는 데에서 “상동성(homology)” 용어를 도입했다고 보고 있다.

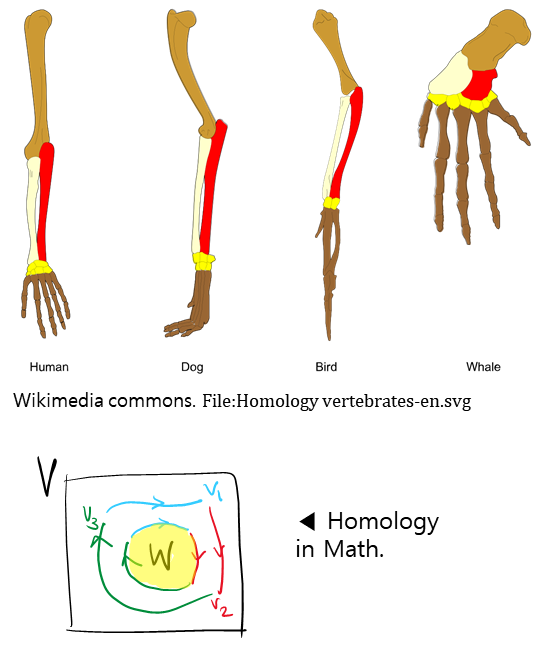
만약 이 생물학적 배경이 (실질적인) 기원이라면, “상동관계” 및 “상동군”이 당시 역사적 맥락을 담은 homologous 및 homology group의 번역언이 될 수 있을 것이다. 이 경우 cohomologous를 “쌍대(켤레?)상동관계” 등으로 자연스럽게 번역할 수 있고, 또 어느 정도 역사적 맥락을 담은 용어라는 장점을 들 수 있겠다.

다만 이 경우 homology algebra는 “상동대수학”이 될 터인데, 기하학적인 맥락 상 아주 무관한 단어 선정은 아니지만, 점차 생물학적 기원과 동떨어지는 느낌을 막을 수는 없어 보인다.

대수적 맥락에서

앞서는 역사적 맥락을 짚어보며, 호몰로지라는 말에서 느낄 법한 내용에 대해 알아보았다. 그러나 최근 호몰로지의 대수적 의미에 대해 다시 생각해 볼 만한 자료를 소개받아, 그 내용과 그에서 따른 생각을 정리한다.

지난 달 공개된, Ravi Vakil의 호몰로지 그림책의 pp. 25-26에 따르면, (코)호몰로지 군은 “겹친 영역을 쳐내고 남은 것”을 그려낸 개념으로 볼 수 있다.

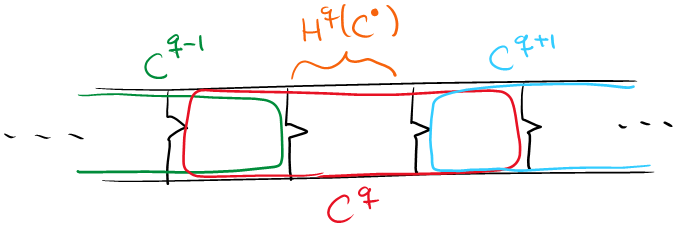
즉 주변 군과의 차이에 해당하는 영역만 정확히 잘라낸 결과가 코호몰로지군이라 볼 수 있는 것이다.

따름생각

이 점을 들어, 상대적 차이를 추려낸 군으로써 “대차군(對差群)”이라는 용어를 생각해 보았다.

이는 호몰로지 대수에 대해, “대차군론” 내지는 “대차대수학”과 같은 대안을 제시하면서, 동시에 이어지는/상대적인 차이를 대수적으로 바라본다는 인상을 담을 수 있기를 기대한 것이다.

다만 기대한 효과가 유효한지는 차치하더라도, 이 용어선정에도 여러모로 문제가 있다. 주변 군과의 차이에 관심을 둔다는 점에서는 코호몰로지나 호몰로지나 동일하기에, (아무리 호몰로지를 “음수 차수 코호몰로지”로 볼 수 있다 해도) 두 개념 모두 “대차군”이라는 용어를 쓸 수밖에 없고, 나아가 기하학적인 맥락이 아예 사라진 용어인 탓에, 둘이 굳이 쌍대여야 하는가에 대한 의문 또한 남게 된다.

굳이 기하학적인 맥락을 넣고자 “기하대차군” (위상적 호몰로지군) 또는 “형식대차군” (위상적 코호몰로지군) 용어를 도입해 볼 수는 있으나, 결국 둘이 쌍대적임을 드러내지는 못하는 용어에 지나지 않아 보인다.

Update Log

• 220404: Created