A Formula of Hyperbolic Distance

The idea of this post is to (1) introduce a formula to measure a distance on the upper half plane with the ‘standard’ hyperbolic metric, and (2) record some ideas of deriving this.

Preliminaries

I list some basic facts about the upper half plane \(\mathbb{H}=\{z\in\mathbb{C} : \Im z>0\}\) model of the hyperbolic 2-plane.

• To have the curvature $-1$, the standard choice of metric is

• Geodesics in $\mathbb{H}$ are, as figures in $\mathbb{C}$, either upper half circles centered at a real number, or vertical lines (i.e., lines parallel to the imaginary axis).
• Isometries of $\mathbb{H}$ are given as Mobius transforms by real matrices. That is, for each isometry $f\colon\mathbb{H}\to\mathbb{H}$, we have $a,b,c,d\in\mathbb{R}$, $ad\neq bc$, such that

• Fix $z_2\in\mathbb{H}$. The map $z\mapsto(z-z_2)/(z-\overline{z}_2)$ is an isometric map $\mathbb{H}\to\mathbb{D}$ to the Poincare disk model. The map sends $z_2\in\mathbb{H}$ to $0\in\mathbb{D}$.
• The hyperbolic circles in $\mathbb{D}$, centerd at $0\in\mathbb{D}$, are same as Euclidean circles with the same center. (For other centers, the descriptions get more complicated.)

Distance Formula

Morally, one can find the hyperbolic distance between $z_1,z_2\in\mathbb{H}$ by sketching the hyperbolic geodesic between them, and use the formula

to evaluate the distance. This is nice, except that it requires an unfeasible amount of computations.

So we introduce a ‘formula-wise’ way to find the distance, which reads as follows.

\begin{equation} \label{eqn:hyperbolic-distance} \mathsf{dist}_{\mathbb{H}}(z_1,z_2)=\log\left(\frac{|z_1-\overline{z}_2|+|z_1-z_2|}{|z_1-\overline{z}_2|-|z_1-z_2|}\right). \end{equation}

To see how the formula works, here is a picture:

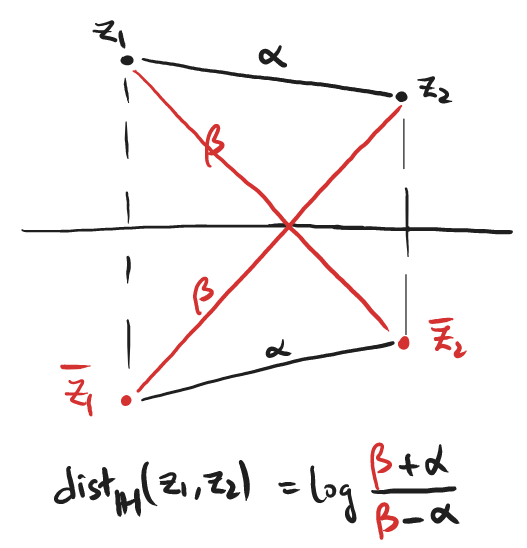
Although the distance formula does not look symmetric in $z_1$ and $z_2$, the symmetry evidently follows from the figure above. (An algebraic verification is not too hard, though.)

We aim to prove \eqref{eqn:hyperbolic-distance} in this post.

Idea

Fix $z_2\in\mathbb{H}$. The idea of the proof is to think of the locus of points $z_1\in\mathbb{H}$ that are claimed to be ‘equidistanced’ from $z_2$. If such loci are hyperbolic circles, then we can claim the relation with the actual hyperbolic distances.

To elaborate, define the quantity

\begin{equation} \label{eqn:exp-hyperbolic-distance} D(z_1,z_2) = \frac{|z_1-\overline{z}_2|+|z_1-z_2|}{|z_1-\overline{z}_2|-|z_1-z_2|}. \end{equation}

It is not hard to show that the quantity $D(z_1,z_2)$ always stays in $[1,\infty)$, with $D(z_1,z_2)=1$ iff $\vert z_1-z_2\vert =0$ iff $z_1=z_2$.

Fix $D_0>0$. If the set of points $z\in\mathbb{H}$ with $D(z,z_2)=D_0$ forms a hyperbolic circle, then we infer that its (hyperbolic) radius $\rho=\mathsf{dist}_\mathbb{H}(z,z_2)$ should be determined by $D_0$. Then we study the relation $\rho=\rho(D_0)$ by, say, plugging in special points like $z=z_0+it$ ($t$ a real number, $t\in(0,\infty)$).

Computer Sketches

Before diving into the proof, we introduce some computer sketches that supports the idea. Setting $z_2=i$, we sketch the loci of $D(z,i)=2,3,4,5,6$ as follows. desmos demo

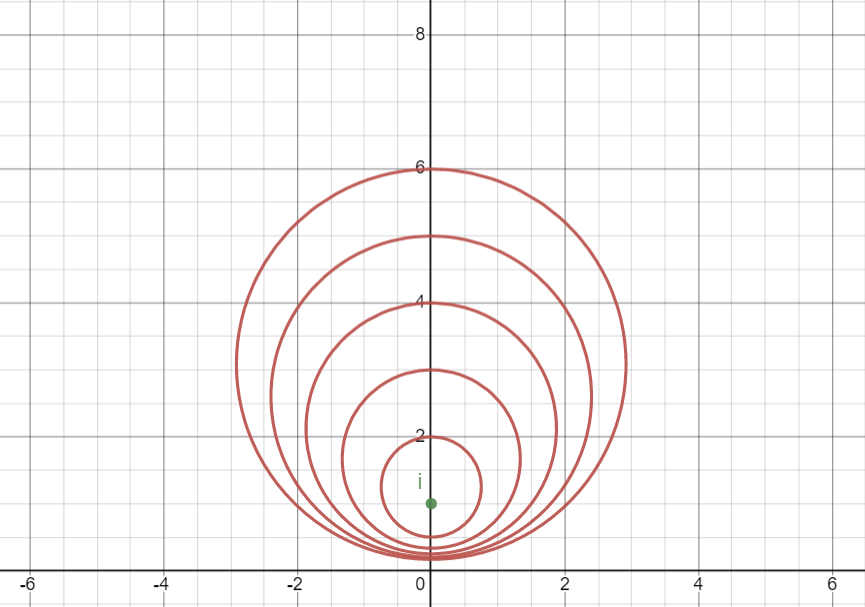
These set of circles are known to be concentric circles, with center $z_2=i$, in the hyperbolic plane. Indeed, if one transforms this to the Poincare disk, via the map $z\mapsto(z-i)/(z+i)$, then we get the following picture.

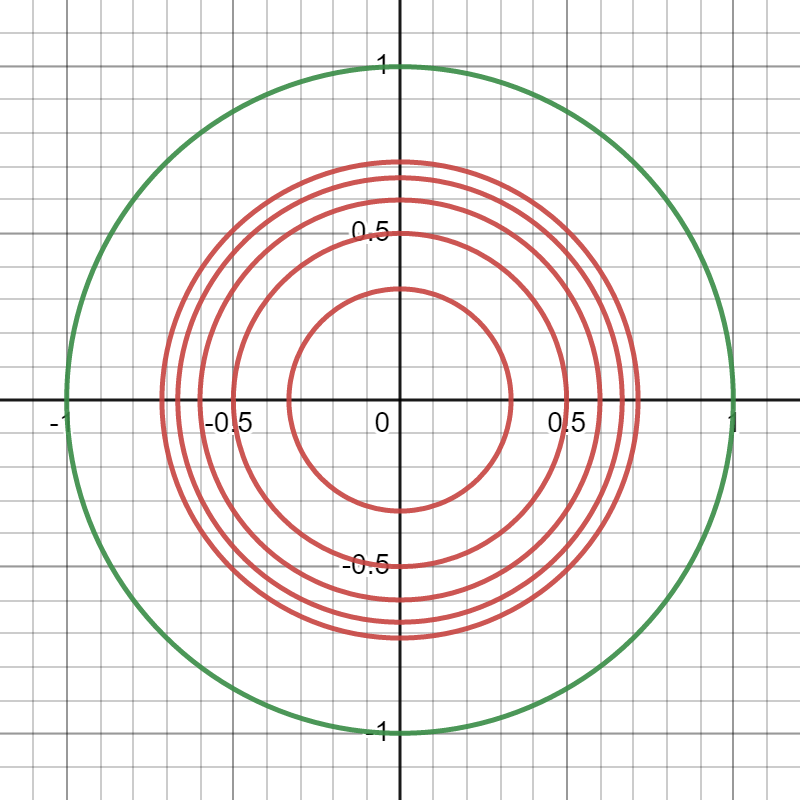
As noted above (as a ‘preliminary’), these circles are indeed hyperbolic circles (in the Poincare disk model).

How do we measure the diameters of these circles? Because the transform $z\mapsto(z-i)/(z+i)$ is an isometry, it does not matter whether we measure the distance in $\mathbb{D}$ or $\mathbb{H}$. But for $\mathbb{H}$, we know that (with $z_2=i$) the point $z=Di$ lies on the circle (i.e., $D(Di,i)=D$), and it is quite handy to measure the distance from $z_2=i$ to $z=Di$: simply recall that the curve $\gamma(t)=it$, $1\leq t\leq D$, is the geodesic from $z_2$ to $z$, and evaluate the length

Now this aready proves the formula \eqref{eqn:hyperbolic-distance} for a special case of $z_2=i$. Arguments below are just meant to be a generalization of this.

Hyperbolic circles

Declare the map $\phi\colon\mathbb{H}\to\mathbb{D}$ by

Then this $\phi$ is an isometry that sends $z_2\mapsto 0$. Furthermore, the quantity \eqref{eqn:exp-hyperbolic-distance} may be written as

Thus the set of points $z\in\mathbb{H}$ with $D(z,z_2)=D_0$ is thus sent to, via $\phi$, the set of points $w\in\mathbb{D}$ with $\vert w\vert=\frac{D_0-1}{D_0+1}$. That is, the locus is mapped to a (hyperbolic) circle in $\mathbb{D}$, centered at $0$. As $\phi$ is an isometry, this implies that the points $z\in\mathbb{H}$ with $D(z,z_2)=D_0$ form a hyperbolic circle (in $\mathbb{H}$).

This means that the quantity \(\mathsf{dist}_\mathbb{H}(z,z_2)\) is constant if $D(z,z_2)$ is constant, i.e., $\mathsf{dist}_\mathbb{H}(z,z_2)$ is a function of $D(z,z_2)$. We declare a function $\rho\colon[1,\infty)\to[0,\infty)$ and write \(\rho(D(z,z_2))=\mathsf{dist}_\mathbb{H}(z,z_2)\) for that status.

Relation

Now we plug in $z=z_2+it$, where $t>0$. Then the hyperbolic geodesic connecting $z_2$ to $z$ is given as a curve $\gamma(s)=z_2+is$, $0\leq s\leq t$. There, we compare

and

So given any input $D_0\in[1,\infty)$, we can write this as $D_0=1+t/\Im z_2$, and we have

We thus conclude that,

which is essentially \eqref{eqn:hyperbolic-distance}, as required.

Update Log

• 220621: Created