Cone Model for Vieta Actions on Tropical Markov Cubics
Published:
A comment to my recent work, regarding an alternative model for describing the “holomorphic parameters” case.
Summary of the Work
Quite recently, I have uploaded a work that focuses on some algebraic dynamics on an affine surface, called Markov cubics:
\[S_{ABCD}\colon X^2+Y^2+Z^2+XYZ=AX+BY+CZ+D,\]where A, B, C, D are parameters. As seen in the equation, this surface is quadratic in each variable X, Y, and Z, hence defines involutions (called Vieta involutions) that ‘flips’ the quadratic solutions:
\[\begin{array}{rl} s_1(X,Y,Z) &= (-YZ+A-X, Y, Z), \\ s_2(X,Y,Z) &= (X, -XZ+B-Y, Z), \\ s_3(X,Y,Z) &= (X, Y, -XY+C-Z). \end{array}\]Consider the group $\Gamma=\langle s_1,s_2,s_3\rangle$ generated by these involutions. Then we are interested in how Γ acts on the surface $S_{ABCD}$.
The main theorem of (J. 2023) is about how Γ acts tropically on the surface.
Theorem. Suppose a Markov cubic is defined on a non-archimedean field $(K,\mathrm{val})$. Consider the tropicalization $\mathbf{Trop}(S_{ABCD})$ of it and the tropical Vieta actions
\[\begin{array}{rl} \mathrm{trop}(s_1)(x,y,z) &= \left(\min(2y,2z,b+y,c+z,d)-x, y, z\right), \\ \mathrm{trop}(s_2)(x,y,z) &= \left(x,\min(2x,2z,a+x,c+z,d)-y,z\right), \\ \mathrm{trop}(s_3)(x,y,z) &= \left(x,y,\min(2x,2y,a+x,b+y,d)-z\right). \end{array}\]Then there is an invariant subset, called a skeleton,
\[Sk=\left\{(x,y,z)\in\mathbf{Trop}(S_{ABCD}) : x+y+z=\min\left(\begin{array}{l}2x,2y,2z,d, \\ a+x,b+y,c+z\end{array}\right)\right\}, \label{eqn:skeleton}\]admitting a tropical action $\Gamma=\langle s_1,s_2,s_3\rangle\curvearrowright Sk$ and its description, as follows.
- (Meromorphic param.) If one of the parameters A, B, C, D has a negative valuation, then there is an open dense invariant subset U in the skeleton whose Γ-action is conjugate to the (∞,∞,∞)-triangle group action on the hyperbolic plane.
- (Holomorphic param.) If all of the parameters A, B, C, D have nonnegative valuations, then by spherically projecting the skeleton \((Sk\setminus\{\mathbf{0}\})/\mathbb{R}_{>0}\), the Γ-action is conjugate to the (∞,∞,∞)-triangle group action on the boundary of the hyperbolic plane.
When one of the parameters has a negative valuation (called meromorphic parameters in the paper), the picture goes like the one below. There, the claimed open subset U equals the entire orbit of the triangle in the middle.
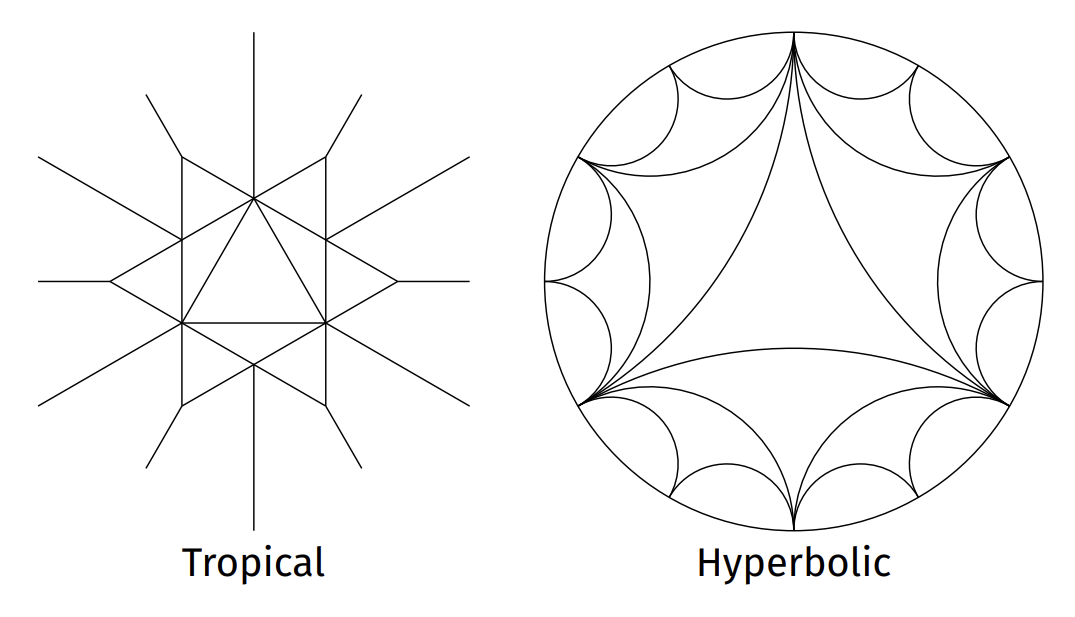
When all the parameters have nonnegative valuations (called holomorphic parameters in the paper), the picture goes as one below. Focus on how rays are placed on the ‘tropical’ side and how vertices are placed on the ‘hyperbolic’ side.
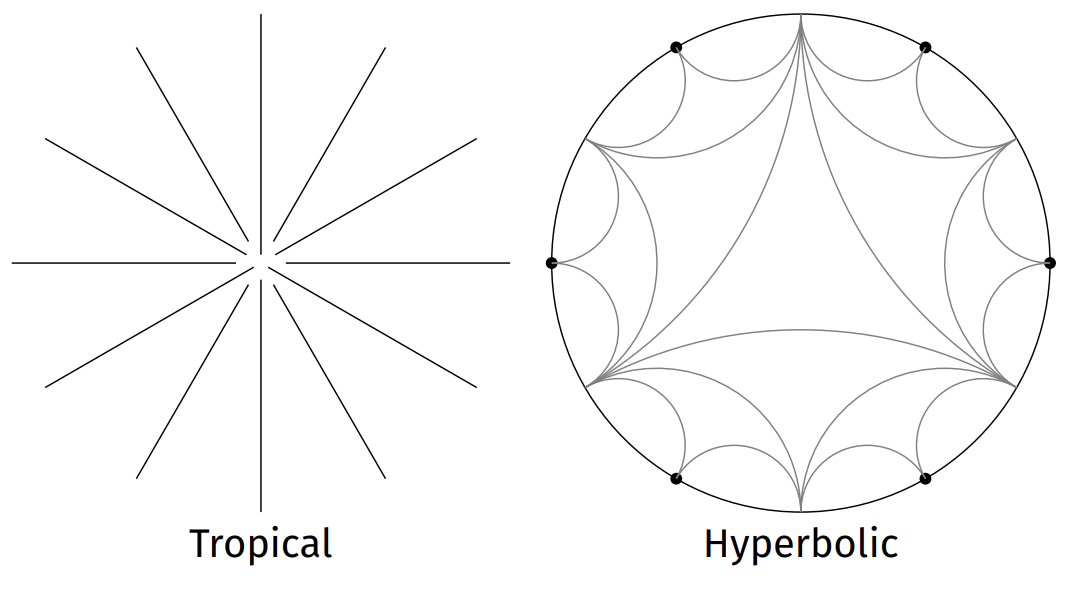
So the results use hyperbolic reflections and tessellations (called a Farey tessellation) to model the tropical action, but how we understand holomorphic parameters is “1-dimension lower” than the meromorphic case. In particular, we dismiss what happens on each ray as we go along the dynamics (which usually expands to infinity, but we can still question “at which rate?”).
This led me to ask the following question.
Question. Can I describe the tropical actions for the holomorphic case, without lowering a dimension?
Uniform Model for Holomorphic Parameters
One aspect that holomorphic parameters enjoy is that the skeleton, the key invariant set, is uniform in the following sense.
Proposition 1. If all parameters have nonnegative values, then the skeleton (see \eqref{eqn:skeleton}) is precisely the union of following planar cones:
- \[C_1=\{(x,y,z)\in\mathbb{R}^3 : x=y+z,\ x,y,z\leq 0\}\]
- \[C_2=\{(x,y,z)\in\mathbb{R}^3 : y=z+x,\ x,y,z\leq 0\}\]
- \[C_3=\{(x,y,z)\in\mathbb{R}^3 : z=x+y,\ x,y,z\leq 0\}\]
Furthermore, the Vieta involutions tropically act as follows:
- $\mathrm{trop}(s_1)(x,y,z) = \left(\min(2y,2z)-x,y,z\right)$
- $\mathrm{trop}(s_2)(x,y,z) = \left(x,\min(2x,2z)-y,z\right)$
- $\mathrm{trop}(s_3)(x,y,z) = \left(x,y,\min(2x,2y)-z\right)$
So no matter whether $(\mathrm{val}(A),\mathrm{val}(B),\mathrm{val}(C),\mathrm{val}(D))$ is (0,0,0,0), (∞,∞,∞,2), (1.2,1.3,0.5,∞), etc., we always see the same skeleton and Vieta actions on it.
Geometrically, this skeleton could be understood as a tetrahedral cone. Consider a regular tetrahedron in $\mathbb{R}^3$ whose vertices are (0,0,0), (0,-1,-1), (-1,0,-1), and (-1,-1,0). Then the cone generated by the tetrahedron will lie on the (-,-,-)-octant and have 3 planar facet. Remove the solid part of the cone, and that will be the skeleton.
The tropical Vieta involutions have some geometric idea on how they work, which appear as some shear transformations. Precisely describing these shears requires some special coordinates and can be best consulted by (J. 2023), Sec. 5.
The question above is then really asking, whether the above cone description is the easiest description we can expect. It turned out to be no, thanks to a well-known Markov cubic with holomorphic parameters.
The Cayley Cubic
For the parameter A=B=C=0 and D=4, the Markov cubic is called a Cayley cubic and it takes a special role in the study of representations of free groups by 2x2 matrices. We list some key lemmas that will help us follow the idea.
Lemma. Let $A,B$ be 2x2 matrices (on any ring) whose determinants are all 1. Then we have the following identity.
\[[A,B]=ABA^{-1}B^{-1} \\ =xA+y(ABA^{-1})+(z-xy)AB-I, \label{eqn:230730-1}\]where $x=\operatorname{tr}A,y=\operatorname{tr}B,z=\operatorname{tr}AB$, and I is the identity matrix.
Proof
(proof) It is a straightforward computation using the Cayley--Hamilton theorem. The Cayley--Hamilton theorem (and the determinant condition) gives us identities like $A^2=xA-I$ or $B^{-1}=y-B$, etc., and thus we expand $$\begin{array}{rl} [A,B] &= AB(x-A)(y-B) \\ &= xyAB-yABA-xAB^2+(AB)^2 \\ &= xyAB-y(ABA^{-1})A^2-xA(yB-I)+zAB-I \\ &= xA-y(ABA^{-1})(xA-I)+zAB-I \\ &= xA-xyAB+y(ABA^{-1})+zAB-I \\ &= xA+y(ABA^{-1})+(z-xy)AB-I \end{array}$$ and prove the demanded. $\square$
The so-called Fricke identity
\[\operatorname{tr}[A,B]=x^2+y^2+z^2-xyz-2\]is an immediate consequence of \eqref{eqn:230730-1}. Furthermore, if we set $\operatorname{tr}[A,B]=2$, then in terms of $x=\operatorname{tr}A,y=\operatorname{tr}B,z=\operatorname{tr}AB$, we have the following polynomial relation:
\[x^2+y^2+z^2-xyz=4. \label{eqn:230730-2}\]This resembles the equation for the Cayley cubic
\[S_{0004}\colon X^2+Y^2+Z^2+XYZ=4,\]and indeed by the coordinate transform $(x,y,z)=(-X,-Y,-Z)$ we see that $S_{0004}$ is the surface defined by the relation \eqref{eqn:230730-2}.
The setup $\operatorname{tr}[A,B]=2$ gains attention by the following
Lemma. Let $A,B$ be 2x2 matrices over an algebraically closed field whose determinant is 1. If $[A,B]$ has trace 2, then there is an appropriate basis in which one can represent the matrices A, B into the following form:
\[A=\begin{bmatrix} u & \ast \\ 0 & u^{-1} \end{bmatrix},\quad B=\begin{bmatrix} v & \ast \\ 0 & v^{-1} \end{bmatrix}. \label{eqn:230730-3}\]
Proof
(proof) Note that this is equivalent to the claim that A, B have a common eigenvector $\vec{x}_1$ (the first basis vector). If $\vec{x}_1$ is a common eigenvector of both A and B, taking any linearly independent vector $\vec{x}_2$, it is not hard to see that A, B takes the demanded upper triangular form.
By Jordan decomposition, one can see that $[A,B]$, a matrix with determinant 1 and trace 2, is either the identity matrix or a unipotent matrix (identity plus a nilpotent matrix).
For the former, this means that A, B are commutative. Take any eigenvector $\vec{x}_1$ of A (it exists by algebraic closedness), so that $A\vec{x}_1=u\cdot\vec{x}_1$. Then we have $$(A-uI)B\vec{x}_1=B(A-uI)\vec{x}_1(=\vec{0}),$$ hence $B\vec{x}_1\in\ker(A-uI)$. If the kernel is 1-dimensional then $B\vec{x}_1$ must be proportional to $\vec{x}_1$ (i.e., an eigenvector of B). If the kernel is 2-dimensional then A is a nonzero scalar matrix (could be I, could be -I) and we switch to re-choose $\vec{x}_1$ to be an eigenvector of B.
For the latter, observe that
- $A^{-1}B^{-1}AB=(BA)^{-1}[A,B](BA)$
- $A^{-1}B^{-1}AB\vec{y}=\vec{y}$, i.e., $(AB-BA)\vec{y}=0$.
Denote $N=AB-BA$. Then there is a basis in which one can represent $N=[\begin{smallmatrix} 0 & 1 \\ 0 & 0 \end{smallmatrix}]$. Observe further that
- $BAB^{-1}-A=-NB^{-1}$ has trace 0, and
- $ABA^{-1}-B=NA^{-1}$ has trace 0.
Because
\[AB=\begin{bmatrix} uv & \ast \\ 0 & (uv)^{-1} \end{bmatrix}\]according to the format \eqref{eqn:230730-3}, the lemma tells us that whenever $(X,Y,Z)$ lies on the surface $S_{0004}$, there are nonzero numbers u, v such that
\[\begin{array}{rl}(X,Y,Z)&=\Phi(u,v) \\ &:=\left(-u-\dfrac1u,-v-\dfrac1v,-uv-\dfrac1{uv}\right).\end{array}\]Over a field K, The map Φ defined above shall be understood as a quotient of the (surjective!) map
\[\begin{array}{rl} \widetilde{\Phi}\colon(K^\times)^2 &\to S_{0004}(K), \\ (u,v) &\mapsto \left(-u-\dfrac1u,-v-\dfrac1v,-uv-\dfrac1{uv}\right). \end{array}\]Some algebraic manipulations indicates that the ‘kernel’ of $\widetilde{\Phi}$, i.e., the set of pairs (u,v), (u’,v’) such that $\widetilde{\Phi}(u,v)=\widetilde{\Phi}(u’,v’)$, is $(u’,v’)=(u,v)\text{ or }(u^{-1},v^{-1})$. This leads us to think the monomial action by $-I$, i.e.,
\[-I.(u,v)=(u^{-1},v^{-1}),\]and reduce $\widetilde{\Phi}$ to the map
\[\begin{array}{rl} {\Phi}\colon(K^\times)^2/\langle-I\rangle &\to S_{0004}(K), \\ [(u,v)] &\mapsto \left(-u-\dfrac1u,-v-\dfrac1v,-uv-\dfrac1{uv}\right). \end{array} \label{eqn:230730-4}\]By this we have an isomorphism between the Cayley cubic $S_{0004}$ and the quotient ‘variety’ $(K^\times)^2/\langle -I\rangle$.
Dynamics
The “algebraic torus” $(K^\times)^2$ has a natural $\mathrm{GL}_2(\mathbb{Z})$-action
\[\begin{bmatrix} a & b \\ c & d \end{bmatrix}.(u,v)=(u^av^b,u^cv^d),\]called the monomial action. This action descends to $(K^\times)^2/\langle-I\rangle$ as well, which is really a $\mathrm{PGL}_2(\mathbb{Z})(=\mathrm{GL}_2(\mathbb{Z})/\langle-I\rangle)$-action. The PGL group contains a copy of $\Gamma=\langle s_1,s_2,s_3\rangle$ by
\[\begin{array}{rl} \Gamma & \hookrightarrow \mathrm{PGL}_2(\mathbb{Z}), \\ s_1 &\mapsto \begin{bmatrix} 1 & 2 \\ 0 & -1 \end{bmatrix}, \\ s_2 &\mapsto \begin{bmatrix} -1 & 0 \\ 2 & 1 \end{bmatrix}, \\ s_3 &\mapsto \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}. \end{array}\label{eqn:230730-5}\]To be rigorous, this should be understood as an embedding of the 3-fold free product of the group of order 2, together with a separate theorem that says Γ is also such a free product. But I did not want to introduce additional notation for the free product.
Then the following comes from simple computations.
Lemma. The map Φ in \eqref{eqn:230730-4} respects the Γ-actions, where the Γ-action on $(K^\times)^2/\langle-I\rangle$ is the monimal action (provided that we view Γ as a subgroup of $\mathrm{PGL}_2(\mathbb{Z})$ according to the embedding \eqref{eqn:230730-5}).
Tropical
Given an affine variety $\mathcal{X}\subset\mathbb{A}^n$ over a non-archimedean field K, we define its tropicalization as
\[\mathbf{Trop}(\mathcal{X}) = \overline{\left\{\left(\mathrm{val}(X_i)\right)_{i=1}^n\in\mathbb{R}^n : \left(X_i\right)_{i=1}^n\in\mathcal{X}(K)\right\}}.\]So we understand that the tropicalization is essentially listing all possible valuations of K-points. Having this data, we can think an analogous notion for the quotient $(K^\times)^2/\langle -I\rangle$.
Consider the valuation map
\[\begin{array}{rl} (K^\times)^2 &\to \mathbb{R}^2, \\ (u,v) &\mapsto (\mathrm{val}(u),\mathrm{val}(v)). \end{array}\]This induces a map $(K^\times)^2/\langle -I\rangle \to \mathbb{R}^2/\pm 1$, and respects the monomial $\mathrm{PGL}_2(\mathbb{Z})$-action (to linear ones). Hence $\mathbb{R}^2/\pm 1$ has a linear Γ-action given by \eqref{eqn:230730-5}.
This rough ‘tropicalization’ of the quotient connects to the tropicalization of the Cayley cubic $S_{0004}$ as follows. One has
\[\mathrm{val}\left(u+\frac1u\right)\]equal to $-\vert\mathrm{val}(u)\vert$ if val(u) is nonzero, and a nonnegative number if val(u) is zero. If we consider a variant of ReLU function, $\mathrm{ReLU}(x)=\min(x,0)$, then we obtain a formula
\[\mathrm{ReLU}\left(\mathrm{val}\left(u+\frac1u\right)\right)=-|\mathrm{val}(u)|.\label{eqn:230730-6}\]This ReLU is closely related with the skeleton, in the following way. If we apply the ReLU function (coordinatewise) to the entire tropicalization of the Cayley cubic, we have a retract to the skeleton:
\[Sk\overset\subset\hookrightarrow\mathbf{Trop}(S_{0004})\overset{\mathrm{ReLU}}\twoheadrightarrow Sk.\]Remark (TechNote). The ReLU function contracts everything into the (-,-,-)-octant, and in terms of the tropical polynomials, this octant only cares about monomials 2x, 2y, 2z, and x+y+z, in case of holomorphic parameters. Such an observation is not the case for meromorphic parameters!
It is now natural to ask, how does the isomorphism $\Phi\colon(K^\times)^2/\langle -I\rangle\to S_{0004}$ ‘tropicalize.’ That is, whether we have a good arrow in the following diagram:
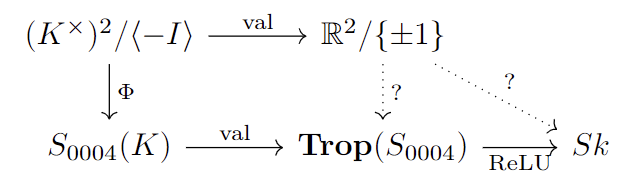
The relation \eqref{eqn:230730-6} indicates which arrow should be drawn.
Proposition 2. Let $\varphi\colon\mathbb{R}^2/\pm 1\to Sk$, $\varphi[(x,y)]=(-\vert x\vert,-\vert y\vert,-\vert x+y\vert)$. This φ fits in the above commutative diagram. Furthermore, φ is a homeomorphism that respects Γ-actions.
The hardest part of the above proposition is showing homeomorphicity, which requires describing how $\varphi^{-1}$ is defined on each subset $C_i\subset Sk$, i=1,2,3 (see proposition 1 for what these subsets are).
An Updated Model
Proposition 2 de facto resolves the initial question. But we clearly state it for sake of later references.
Theorem. Consider the skeleton of a Markov cubic defined over a non-archimedean field, with holomorphic parameters. Then the tropicalized Vieta action on the skeleton is conjugate to the following action on the antipodal quotient of the Euclidean plane:
\[\left\langle s_1=\begin{bmatrix} 1 & 2 \\ 0 & -1 \end{bmatrix},s_2=\begin{bmatrix} -1 & 0 \\ 2 & 1 \end{bmatrix},s_3=\begin{bmatrix} -1 & 0 \\ 0 & 1\end{bmatrix}\right\rangle\curvearrowright\mathbb{R}^2/\pm 1.\]
Acknowledgement
The idea of studying Cayley cubic is due to Serge Cantat. Details of the linear algebra lemmata were established by various helps from Seok Hyeong Lee, Minju Lee and Simion Filip.
Update Log
- 230730: Created