진자운동으로 타원곡선 샘플링하기
Published:
정리. 길이 L, 중력가속도 g, 질량 m인 단진자의 운동방정식 $\ddot{\theta}=-\frac{g}{L}\sin\theta$이 주기 T를 가진다 하자. 이 때 최대 각도를 $\theta_0$라 써, $\lambda=(1-\cos\theta_0)/2$라 하자. 또, $u=(1-\cos\theta)/2$를 높이 함수라 하자. 그러면 시간 t가 구간 [0,T] 안에서 균등하게 임의로 골라질 때, 높이함수와 그 미분 $(u(t),\dot{u}(t))$은 타원곡선 $E_\lambda\colon y^2=4x(x-1)(x-\lambda)$의 (항등원 없는 연결성분 위로 제한된) Haar 측도를 따른다.
맥락
위 정리의 기술만큼이나, 왜 이 이야기를 꺼내는지에 대한 맥락 또한 타원곡선에 대한 어느 정도의 이해를 필요로 한다. 이 일련의 이야기가 이미 익숙하다면 바로 아래의 질문으로 넘어가기를 바란다.
타원곡선 (일반론)
사영평면 $\mathbb{P}^2$ 위에 정의된 3차 곡선 중 매끈한 것, 곧 특이점이 없는 것을 생각해 보자.1 여기에 곡선 위의 점이 추가로 주어질 때, 곡선과 점의 순서쌍 $(C,o)$을 타원곡선이라 부른다.
이 순서쌍에는 점 o를 항등원으로 삼는 군 구조를 만들 수 있다. 점 $p,q\in C$의 덧셈은 다음 순서를 따른 결과로 본다.
- 두 점 p,q를 잇는 직선을 만든다. 그러면 곡선 C와 만나는 3번째 점 r을 잡을 수 있다.
(곡선 C를 정의하는 수식으로부터 직선 위의 (선형) 매개변수에 대한 3차방정식을 얻는데, 이미 점 p,q로부터 근 2개를 알고 있으므로 다항식의 나눗셈으로 3번째 점을 찾을 수 있다.) - 두 점 r,o를 잇는 직선을 만든다. 그러면 곡선 C와 만나는 3번째 점 s를 잡을 수 있다. 그 점이 두 점 p,q의 덧셈이다. (곧, $s=p+q$.)
이 연산이 (1) 교환법칙을 만족하고 (2) 점 o를 항등원으로 가진다는 것까지는 그래도 쉽게 볼 수 있지만, (3) 결합법칙 $(p+q)+r=p+(q+r)$과 (4) 역원을 가진다는 것은 “어렵진 않아도 성가신” 종류의 확인 작업이 필요하다 (Silverman & Tate 2015, 1.2절 p. 14)(Reid 2013, Figure 2.3, p. 41).2 하여간, 요는 타원곡선 (C,o,+)이 아벨군을 이룬다는 것이다.
곡선 C의 점 중 복소수 좌표를 가진 것을 모으면,3 이 아벨군이 복소평면 $\mathbb{C}$를 격자군 \(\Lambda=\mathbb{Z}.\{\omega_1,\omega_2\}\)으로 나눈 몫군과 동형임이 알려져 있다 (Silverman 2009, VI.5절 따름정리 5.1.1). 이 몫군 $\mathbb{C}/\Lambda$을 그림으로 그려내면 아래와 같은 식이다. 그림 출처
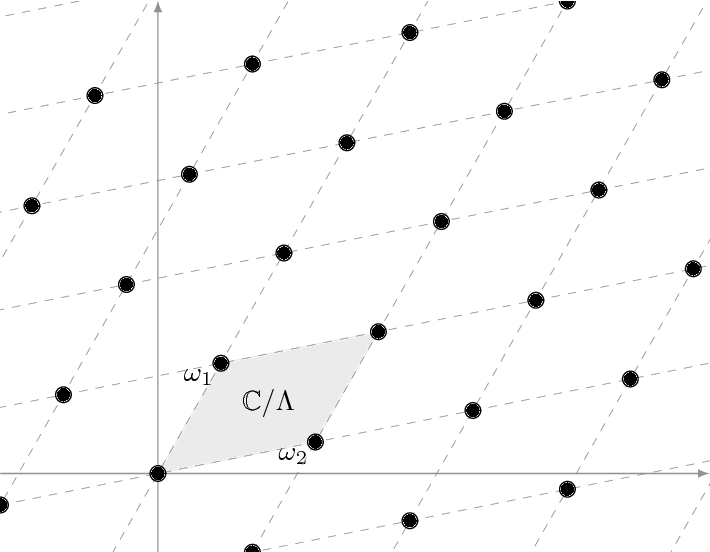
곧, $\omega_1,\omega_2$이 좌표평면 $\mathbb{R}^2$ 위의 기저처럼 나타나기에, 몫군 $\mathbb{C}/\Lambda$을 다음과 같이 사각형의 양 변을 이은 그림으로 그려낼 수 있다. 그림 출처

혹여 곡선 C가 매끈한 실계수 3차 다항식으로 정의된 곡선이면, 그 위의 점 중 실수 좌표를 가진 것 또한 몫군 $\mathbb{C}/\Lambda$ 안의 부분군이라 예상할 수 있다. 어떤 부분군이 여기서 나타날 수 있을까?
1. 수식으로 쓰면 이런 식이다. F(X,Y,Z)=0이 곡선을 정의하는 다항식이라 하자. 그러면 곡선 위의 임의의 점 (X0,Y0,Z0)에 대해, F의 편미분 중 점 (X0,Y0,Z0)에서 계산할 때 0이 아닌 것이 있을 때, 이 곡선을 매끈하다라 정의한다. 곧, F=0 및 ∇F=0에 공통해가 없는 것을 말한다. ↩
2. Silverman 2009의 경우 III.2절에서 군 구조를 다루기는 하지만, 항등원 o가 변곡점이어야 하는 듯한 인상을 주게끔 쓰여 있다. 때문에 이러한 오해와 무관하게 군 구조를 이해할 수 있는 문헌을 골라 인용하였다. 다만 Silverman의 책 자체로도 이미 많은 주제를 잘 다루고 있기에, 이 글의 다른 부분에서는 해당 책을 자주 인용할 것이다.↩
3. 당연히 곡선을 정의하는 수식 F(X,Y,Z)=0이 복소수 계수를 가진다고 가정한다. 아닐 경우 유한 체라던가, 복소수보다 큰 체 등등 계수가 이상한 곳에 있는 불상사가 발생할 수 있다. ↩
타원곡선 (Weierstrass 형식)
한편 으레 타원곡선이라 할 때 등장하는 수식
\[y^2=x^3+ax+b\]은 Weierstrass 형식의 타원곡선이라 부르며, 굳이 사영평면 위에서의 정의로 보자면
\[Y^2Z=X^3+aXZ^2+bZ^3\]꼴 수식으로 정의된 곡선과 점 $o=[0:1:0]$의 순서쌍으로 볼 수 있다. (보다시피 사영평면 위에서의 정의가 이 곡선이 3차곡선임을 보다 더 잘 볼 수 있기도 하다.)
한편으로, 이 곡선 위의 어지간한 점은 사영좌표 [X:Y:Z]로 쓸 때 Z≠0인 점으로 나타나며, 굳이 Z=0인 점을 찾는다면 $X^3=0$에서 [0:1:0]만 그런 점이 된다는 것을 알 수 있다. 그래서 Weierstrass 형식만을 볼 때에는 굳이 사영평면을 볼 이유가 거의 없으며, 무한점은 단 한 점만 고려해도 된다. 곧,
Weierstrass 형식의 타원곡선은 무한점 [0:1:0]과 좌표평면 상의 곡선 $y^2=x^3+ax+b$으로 이뤄져 있다.
나아가, 이 형식의 타원곡선은 다음과 같은 그림 표현을 가진다. 그림 출처

매끈하지 않은 $(a,b)=(0,0)$을 배제하면, 큰 틀에서 위 그림은 다음 두 종류로 분류할 수 있다.
- 무한으로 뻗는 곡선 하나와 찌그러진 타원 모양의 닫힌 곡선 하나
- 무한으로 뻗는 곡선 하나
이 때 무한으로 뻗는 곡선의 경우 사영평면 위에서는 무한점 [0:1:0]으로 수렴하는 점이라, 이 무한점을 포함한다고 보면 이 또한 닫힌 곡선이라 볼 수 있다. 위 분류는 대수적으로는 판별식 $\Delta=-(4a^3+27b^2)$의 부호가 양수냐 음수냐에 따라 (혹은 3차방정식 $x^3+ax+b=0$의 실근이 3개냐 1개냐에 따라) 전자 또는 후자가 갈린다만, 요는 위상적으로 보았을 때 실수 위에서의 타원곡선은 항상 닫힌 곡선 둘이거나 (전자, 곧 $\Delta>0$) 하나라고 (후자, 곧 $\Delta<0$) 결론을 맺을 수 있다. (판별식이 0인 경우 매끈한 곡선이 나오지 않기에, 굳이 고려하지 않아도 된다.)
무한점 [0:1:0]을 포함하는 쪽은 (즉 무한으로 뻗는 곡선은) 항등원을 포함하는 연결성분이기에 항등원 연결성분이라 부르며, 타원 꼴 곡선은 그렇지 않기에 항등원 없는 연결성분이라 부른다. 이 때, 각 연결성분을 복소 타원곡선(곧 위 곡선에서 복소수 좌표를 모은 것) 안에서 그린다면, 앞서 본 사각형 그림 안에서 다음과 같은 선분으로 그릴 수 있다.
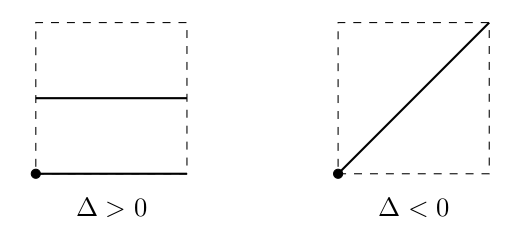
여기서 가로변과 세로변끼리 서로 이어붙인다는 점을 상기하면, 앞서 그린 모든 선분은 결국 양 끝점이 서로 이어붙여질 예정임을 알 수 있다. 나아가, 각 타원곡선은 실수를 정수점으로 나눈 몫군 $\mathbb{R}/\mathbb{Z}$ ($\Delta<0$) 혹은 그 연장 $\mathbb{R}/\mathbb{Z}\times\mathbb{Z}/2\mathbb{Z}$과 ($\Delta>0$) 위상적으로도, 군으로서도 동형이다. 거두절미하고 이를 이른다면,
실수 위에서 정의된 타원곡선은(=실수 계수 다항식으로 정의한 3차 곡선과 실수 좌표의 점의 순서쌍은) 원 하나거나 원 두 개라고 칠 수 있다.
이 때 각각의 원에는, 몫군 $\mathbb{R}/\mathbb{Z}$ 위에서 균일한 확률분포를 도입할 수 있고, 이 확률분포를 (각 연결성분 위에 정의된) Haar 측도라 부른다.그러면 다음과 같은 질문을 던질 수 있다.
질문. 이 Haar 측도를 따르면서 타원곡선 위에 있는 점을 어떻게 샘플링할 수 있을까?
좀 더 노골적으로 말하자면, \((X_1,Y_1), (X_2,Y_2), (X_3,Y_3), \ldots\)이 타원곡선 위의 (Haar 측도를 따르는) 독립동분포(i.i.d.) 확률점(random point)이 되게 하고 싶다면, 어떤 알고리즘을 따라야 하는가?에 대한 질문이기도 하다. 위의 주 정리에 따르면, 다음 얼개를 제시할 수 있다.
답.(얼개) 주기 T인 단진자 운동의 해 $\theta(t)$ 및 그 미분 $\dot\theta(t)$를 알고 있다고 하자. 그러면
\[X=\frac{1-\cos\theta(t)}{2},\quad Y=\frac{\sin\theta(t)}{2}\cdot\dot\theta(t)\]와 같이 잡을 때, 시간 t를 [0,T]에서 균등하게 잡으면 (X,Y)가 바라던 확률점이다.
(구체적으로 어떤 타원곡선에서? 등과 같은 질문은 주 정리에서 답을 찾을 수 있다.)
힘든 길
단진자 운동과의 연관성을 밝히기 전, 이 문제가 단진자 아이디어 없이 어디까지 힘들어질 수 있는지에 대해 먼저 이야기하고자 한다. 시작은 다음 Weierstrass 타원함수다.
\[{\wp (z;\omega _{1},\omega _{2})={\frac {1}{z^{2}}}+\sum _{(m,n)\neq (0,0)}\left({\frac {1}{(z+m\omega _{1}+n\omega _{2})^{2}}}-{\frac {1}{(m\omega _{1}+n\omega _{2})^{2}}}\right)}.\]격자군 \(\Lambda=\mathbb{Z}.\{\omega_1,\omega_2\}=\{m\omega_1+n\omega_2 : m,n\in\mathbb{Z}\}\)을 써서 나타내면, 다음과 같은 식이다.
\[\wp(z;\Lambda)=\frac{1}{z^2} + \sum_{\substack{\gamma\in\Lambda \\ \gamma\neq 0}}\left(\frac1{(z+\gamma)^2} - \frac1{\gamma^2}\right).\]이 타원함수의 기본적인 성질을 아래와 같이 증명 없이 나열한다. 자세한 내용은 (Silverman 2009, VI장) 참고.
명제. Weierstrass 타원함수에 대해 다음이 성립한다.
\[(\wp')^2 = 4\wp^3 - g_2(\Lambda)\wp - g_3(\Lambda).\]
- 함수 $\wp({}\cdot{};\Lambda)$는 $\Lambda$에 주기적이다. 특히, $\wp(z+\omega_1;\Lambda)=\wp(z+\omega_2;\Lambda)=\wp(z;\Lambda)$이다.
- 함수 $\wp(z;\Lambda)$는 정확히 $z\in\Lambda$에서만 계수(order) 2인 극점(pole)을 가진다. 그 z-미분 $\wp’(z;\Lambda)$ 또한 정확히 $z\in\Lambda$에서만 계수 3인 극점을 가진다.
- 함수 $\wp(z;\Lambda)$와 z-미분 $\wp’(z;\Lambda)$는 다음 함수방정식을 만족한다. (여기서 g2 및 g3은 격자군 Λ에 의해 결정되는 값이다.)
따라서 타원곡선 $E_{a,b}$가 다음 수식으로 주여졌다 할 때,
\[E_{a,b}\colon y^2=4x^3-ax-b,\]적당한 격자군 Λ가 있어서 $x=\wp(z;\Lambda)$ 및 $y=\wp’(z;\Lambda)$로 그 복소점을 쓸 수 있다면, 복소좌표점의 모임 $E_{a,b}(\mathbb{C})$를 몫군 $\mathbb{C}/\Lambda$을 통해 볼 수 있을 것이다. 더군다나 Weierstrass 형식의 타원곡선은 무한점이 한 점밖에 없는데, 이는 정확히 $z\in\Lambda$일 때에만 발생한다. 그러므로 함수 $(\wp,\wp’)\colon\mathbb{C}/\Lambda\to E_{a,b}(\mathbb{C})$, $z+\Lambda\mapsto(\wp(z;\Lambda),\wp’(z;\Lambda))$가 어떤 성질을 가지나 물어볼 수 있겠다.
실제로 이 함수는 군으로서도, 위상적으로서도 동형사상이다 (Silverman 2009, VI.5절 따름정리 5.1.1).
복소 균일화 정리. Weierstrass 형식의 타원곡선 $E=(C,o)$가 다음 수식으로 주어졌고,
\[E\colon y^2=4x^3-ax-b,\]그 복소좌표점의 모임을 $E(\mathbb{C})$라 쓰자. 그러면 격자군 $\Lambda$가 유일하게 있어, $(g_2(\Lambda),g_3(\Lambda))=(a,b)$이며, 다음 함수가 위상공간 및 군의 동형사상이다.
\[\begin{array}{rl} (\wp,\wp')\colon\mathbb{C}/\Lambda &\to E_{a,b}(\mathbb{C}), \\ z &\mapsto (\wp(z;\Lambda),\wp'(z;\Lambda)). \end{array}\]
특별히 타원곡선 E의 계수가 실수인 경우, 다음과 같이 덧붙일 말이 생긴다. (기본적으로는 (Silverman 2009, VI장 연습문제 6.7)의 결과이나, 모듈러 형식에 대한 이런저런 결과가 암묵적으로 필요하다.)
실수 균일화 정리. Weierstrass 형식의 타원곡선 $E=(C,o)$가 다음 수식으로 주어졌고,
\[E\colon y^2=4x^3-ax-b,\]그 실수 좌표점의 모임을 $E(\mathbb{R})$라, 판별식을 $\Delta=a^3-27b^2$라 쓰자. 그러면 어떤 양수 $c,\alpha>0$가 있어 다음 복소수 순서쌍이 격자군 $\Lambda$을 생성하며,
\[(\omega_1,\omega_2)=\begin{cases} (c,\sqrt{-1}c\alpha) & (\Delta>0), \\ (c\cdot(\frac12-\sqrt{-1}\alpha),c\cdot(\frac12+\sqrt{-1}\alpha)) & (\Delta<0), \end{cases}\] \[\Lambda=\mathbb{Z}.\{\omega_1,\omega_2\},\]다음 함수가 위상공간 및 군의 동형사상이다. 먼저 판별식이 양수면,
\[\begin{array}{rl} (\wp,\wp')\colon(\mathbb{R}/\mathbb{Z})\times(\mathbb{Z}/2\mathbb{Z}) &\to E_{a,b}(\mathbb{R}), \\ (t,\eta) &\mapsto \left(\wp\left(ct+\frac12\omega_2\eta;\Lambda\right),\wp'\left(ct+\frac12\omega_2\eta;\Lambda\right)\right) \end{array}\]가 그 함수이고, 판별식이 음수면,
\[\begin{array}{rl} (\wp,\wp')\colon\mathbb{R}/\mathbb{Z} &\to E_{a,b}(\mathbb{R}), \\ t &\mapsto \left(\wp(ct;\Lambda),\wp'(ct;\Lambda)\right) \end{array}\]가 그 함수이다.
판별식이 양수일 때의 동형사상이 상당히 복잡해 보인다. 앞서 본 사각형 그림에서 2개의 평행선이 있던 것을 볼 수 있는데, 그 중 아랫변의 경우 평범하게 $\mathbb{R}.\omega_1/\mathbb{Z}.\omega_1=\mathbb{R}/\mathbb{Z}.c$에서 온 변이지만, 윗 변의 경우 허수축 방향으로 “절반만큼”, 곧 $\frac12\omega_2=\frac{\sqrt{-1}}{2}c\alpha$만큼 이동해야 얻을 수 있기 때문이다. 그래서 항등원 연결성분의 경우 (z=0을 지나야 하므로) $[\wp(ct;\Lambda):\wp’(ct;\Lambda):1]$으로 나타나는 한편, 항등원 없는 연결성분의 경우 ($z=\frac12\omega_2$을 지나면서) $[\wp(ct+\frac12\omega_2;\Lambda):\wp’(ct+\frac12\omega_2;\Lambda):1]$로 나타난다. 곧 변수 $\eta\in\mathbb{Z}/2\mathbb{Z}$의 역할은 $\frac12\omega_2$의 스위치인 셈이다.
판별식이 음수인 경우, $\omega_1+\omega_2=c$로부터 $c\cdot(\mathbb{R}/\mathbb{Z})$가 대각선으로 나타나는 것 또한 볼 수 있다. (마치 $\mathbf{i}=(1,0)$ 벡터와 $\mathbf{j}=(0,1)$ 벡터로 만든 정사각형에서 대각선을 보려면 $\mathbf{i}+\mathbf{j}$ 방향으로 나아가야 하는 것처럼!)
Legendre 형식
임의의 실수 위의 타원곡선 $E_{a,b}\colon y^2=4x^3-ax-b$ 중, 실근이 셋인 것은 (즉, 판별식이 양수인 것은) 는 적당한 변수변환을 거치면 다음과 같은 타원곡선으로 변환할 수 있다.
\[E_\lambda\colon y^2=4x(x-1)(x-\lambda).\]위 형식의 타원곡선을 Legendre 형식의 타원곡선이라 부른다. 반대로, 이 Legendre 형식은 다음과 같이 다시 쓸 수 있는데,
\[y^2=4\left(x-\frac{1+\lambda}{3}\right)^3 - \frac43(\lambda^2-\lambda+1)\left(x-\frac{1+\lambda}3\right)-\frac4{27}(\lambda+1)(\lambda-2)(2\lambda-1)\]이러면 $(a,b)=(\frac43(\lambda^2-\lambda+1),\frac4{27}(\lambda+1)(\lambda-2)(2\lambda-1))$에 대해 Eλ와 Ea,b가 같은 곡선이라 볼 수 있다. 앞선 실수 균일화 정리의 경우 격자군을 결정하는 매개변수 c, α>0이 결정된다고만 했지 어떻게 결정된다고는 하지 않았는데, 만약 Legendre 형식의 타원곡선이 주어진다면 적어도 α는 다음과 같이 결정된다. (Wikipedia, τ에 대한 수식, 또는 MathWorld, 수식 (7) 참고.)
역변환 공식. 매개변수 λ가 0<λ<1 안에 있다 하자. 타원곡선
\[y^2 = 4(x')^3 - \frac43(\lambda^2-\lambda+1)x'-\frac4{27}(\lambda+1)(\lambda-2)(2\lambda-1)\]에 실수 균일화 정리를 적용해 얻는 매개변수 α는 다음과 같이 계산할 수 있다. 먼저 제1종 완전한 타원적분
\[K(k)=\int_0^{\pi/2}\frac{d\theta}{\sqrt{1-k^2\sin^2\theta}}\label{eqn:complete-ellipk}\]에 대해, 찾는 매개변수는
\[\sqrt{-1}\alpha = \sqrt{-1}\frac{K(\sqrt{1-\lambda})}{K(\sqrt{\lambda})}\]로 나타난다.
사실 c 또한 $2K(\sqrt{\lambda})$로 나타나기는 한데, 이는 나중에 진자운동에 대한 이야기를 마치면 자연스럽게 나오는 이야기로 소개한다.
그래서 샘플링은?
위의 주 정리와 연관성을 위해, 판별식이 양수인 타원곡선을 생각하고, 그의 항등원 없는 연결성분에 주의해 보자. 앞서 언급한 동형사상 $(\wp,\wp’)$을 활용해서 Haar 측도 샘플링을 하려면 다음과 같이 접근하면 된다.
따름정리. 판별식이 양수인 타원곡선 $E_{a,b}$를 생각하고, Λ, c, α는 앞선 실수 균일화 정리의 것을 쓴다. 시간 $t\in[0,1]$가 균등하게 뽑혔다고 하자. 그러면 $z=ct+\frac12\sqrt{-1}c\alpha$에 대해, 점 $(\wp(z;\Lambda),\wp’(z;\Lambda))$는 $E_{a,b}$의 항등원 없는 연결성분 위의 Haar 측도를 따르는 확률점(random point)이다.
그러므로 만약 $\wp(z;\Lambda)$를 멀쩡히 계산할 수 있다면 구간 [0,1] 위의 균등분포에서 직접 계산하는 것 또한 샘플링의 한 방법일 수 있다. 실제로 $\wp(z;\Lambda)$를 기하급수적으로 구할 수 있는 다음과 같은 식이 있고. (Silverman 2009, C.14절, 혹은 Lang 1987, 4장 2절 46페이지 명제 3 참고.) Jacobi theta 함수에 의한 구현은 stla 참고.
격자군 Λ의 생성원이 ω1=1 및 ω2=τ로 주어지되, τ의 허수부가 양수라 하자. 여기에 $q=\exp(2\pi\sqrt{-1}\tau)$ 및 $u=\exp(2\pi\sqrt{-1}z)$라 하자. 그러면
\[\frac{\wp(z;\Lambda)}{(2\pi\sqrt{-1})^2}=\frac1{12}+\sum_{n\in\mathbb{Z}}\frac{q^nu}{(1-q^nu)^2}-\sum_{n=1}^\infty\frac{2q^n}{(1-q^n)^2},\] \[\frac{\wp'(z;\Lambda)}{(2\pi\sqrt{-1})^3}=2\sum_{n\in\mathbb{Z}}\frac{q^{2n}u^2}{(1-q^nu)^3}+\sum_{n\in\mathbb{Z}}\frac{q^nu}{(1-q^nu)^2}.\]일반적인 격자군의 경우, 만약 ω2/ω1=τ의 허수부가 양수라면, ℘(z;ω1,ω2)=ω1-2℘(z/ω1;1,τ) 및 ℘'(z;ω1,ω2)=ω1-3℘'(z/ω1;1,τ)와 같이 계산한다.
다만 이 타원함수에는 보다 ‘물리적인’ 계산공식이 있기도 하니, 그 쪽 또한 생각해봄직할 뿐이다.
진자운동의 해 θ(t)에서 나타나는 높이함수 u(t)=(1-cos(θ(t)))/2는, 다음 수식을 가진다.
\[u(t)=\frac{1+\lambda}{3}+\wp\left(\frac{\tau}{2}+\frac{t}{T};\Lambda(\lambda)\right).\]
위에서 명시하지 않은 기호가 어떤 것들인지는 다음 절에서 다룬다.
진자운동과 타원곡선
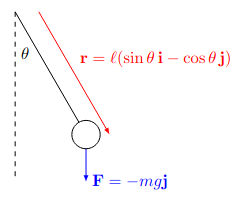
질량 m, 중력가속도 g, 길이 L인 단진자를 생각해 보자. 각 위치 θ는 저점을 0, 최고점을 ±π가 되게끔 잡자. 그러면 토크에 의한 운동법칙으로부터
\[mL^2\ddot{\theta} = \mathbf{r}\times(-mg\mathbf{j})=-mgL\sin\theta\]가 따른다. 적당히 나눌 것을 나누고 나면, 이는 $\ddot\theta=-\frac{g}{L}\sin\theta$로 갈무리된다. 이 때 L/g의 차원이 시간의 제곱이므로, 아예 단위 시간을 $\sqrt{L/g}$로 잡음으로써, L/g=1로 처리할 수 있다.
이제 저점으로부터의 높이의 절반인 $u=(1-\cos\theta)/2$를 생각하자. 그러면 u의 미분은
\[\begin{array}{rl} \dot{u} &= \dfrac12\sin\theta\cdot\dot\theta = -\dfrac{1}{2}\ddot\theta\dot\theta \\ &= -\dfrac{1}{4}\dfrac{d}{dt}(\dot\theta)^2 \end{array}\]를 만족한다. 양변을 적분하면, $u+\frac14(\dot\theta)^2$가 상수임을 알 수 있고, 특히 진자가 최고점 θ0에 이를 때에는 각속도가 0이므로
\[u+\frac14(\dot\theta)^2=\frac12(1-\cos\theta_0)\]이다. 이에 $\lambda=\frac12(1-\cos\theta_0)$라 잡는다. 그러면
\[u-\lambda = -\frac14(\dot\theta)^2=-\frac{(\dot{u})^2}{\sin^2\theta}\]이다. 나아가,
\[u(u-1)= \frac{1-\cos\theta}{2}\cdot\frac{-1-\cos\theta}{2} = \frac{-\sin^2\theta}{4} = \frac{(\dot{u})^2}{4(u-\lambda)}\]로부터, 다음 상미분방정식을 얻는다.
\[(\dot{u})^2 = 4u(u-1)(u-\lambda).\]달리 이르면, 타원곡선 $E_\lambda\colon y^2=4x(x-1)(x-\lambda)$ 및 임의의 시간 t에 대해, $(u(t),\dot{u}(t))$는 이 타원곡선 위의 점이다.
여기서 λ는 일종의 에너지라 볼 수 있다. 최고점에서의 퍼텐셜 에너지가 $mg\cdot L\cdot(1-\cos\theta_0)=2mgL\cdot\lambda$로 나타나는 바, λ가 정규화된 에너지 E/(2mgL)와 같은 것이다.
타원함수 표현
타원곡선 $E_\lambda\colon y^2=4x(x-1)(x-\lambda)$는 앞선 실수 균일화 정리에서 말한 타원곡선 $E_{a,b}$와 약간 다른 형태를 띠고 있다. 그러나 Eλ의 3차식의 근 0, 1, λ의 평균을 통해 변수변환을 하면, 타원곡선 $E_{a,b}$와 형태를 매칭할 수 있긴 하다. 곧, Eλ의 수식을
\[y^2=4\left(x-\frac{1+\lambda}{3}\right)^3 - \frac43(\lambda^2-\lambda+1)\left(x-\frac{1+\lambda}3\right)-\frac4{27}(\lambda+1)(\lambda-2)(2\lambda-1)\]와 같이 쓰면, $(a,b)=(\frac43(\lambda^2-\lambda+1),\frac4{27}(\lambda+1)(\lambda-2)(2\lambda-1))$에 대해 Eλ와 Ea,b가 같은 곡선이라 볼 수 있다. 한편, 다항식 $4x^3-ax-b=0$의 실근은 3개므로 (0,1,λ에 (1+λ)/3을 뺀), Ea,b의 판별식은 양수여야 한다. (실제로 계산하면 $\Delta=16\lambda^2(1-\lambda)^2>0$를 얻는다.)
따라서 어떤 c, α>0가 있어 실수 좌표 (x,y)를, 실수 매개변수 $s\in\mathbb{R}/\mathbb{Z}.c$에 대해 다음과 같이 쓸 수 있다.
\[\begin{array}{rl}(x,y)&=\left(\frac{1+\lambda}{3}+\wp(s;c,\sqrt{-1}c\alpha),\wp'(s;c,\sqrt{-1}c\alpha)\right),\text{ or }\\&\left(\frac{1+\lambda}{3}+\wp\left(s+\frac{\sqrt{-1}}{2}c\alpha;c,\sqrt{-1}c\alpha\right),\wp'\left(s+\frac{\sqrt{-1}}{2}c\alpha;c,\sqrt{-1}c\alpha\right)\right).\end{array}\]만약 $s=s(t)$가 시간 t에 대한 함수고, $u=x$, $\dot{u}=y$가 성립하려면 $s’(t)=1$이어야 한다. 그러므로 s 자체는 시간 t, 혹은 거기에 “위상차만큼” 얼마간 더한 것이어야 한다. 따라서 (시간 “위상차”를 무시하면) 다음 두 근 중 어느 하나가 답이어야 한다.
\[\begin{array}{rl}(u(t),\dot{u}(t))&=\left(\frac{1+\lambda}{3}+\wp(t;c,\sqrt{-1}c\alpha),\wp'(t;c,\sqrt{-1}c\alpha)\right),\text{ or }\\&\left(\frac{1+\lambda}{3}+\wp\left(t+\frac{\sqrt{-1}}{2}c\alpha;c,\sqrt{-1}c\alpha\right),\wp'\left(t+\frac{\sqrt{-1}}{2}c\alpha;c,\sqrt{-1}c\alpha\right)\right).\end{array}\]그러나 전자의 경우 $t\to 0$으로 가면서 $(u,\dot{u})$가 무한점으로 튕겨나가는 것을 본다. 물리적인 관점에서 이것이 말이 안 되는 이야기인 만큼, 후자만 답이 될 수 있다.
뿐만 아니라, 시간 t에 대해 위 함수는 주기 c를 가지는데, 이 주기는 진자의 주기(나누기 단위 시간 $\sqrt{L/g}$)의 절반이다. 이는 타원곡선 Eλ을 따라서 점 $(u,\dot{u})$가 어떻게 변화하는지를 따라가며 확인할 수 있다.
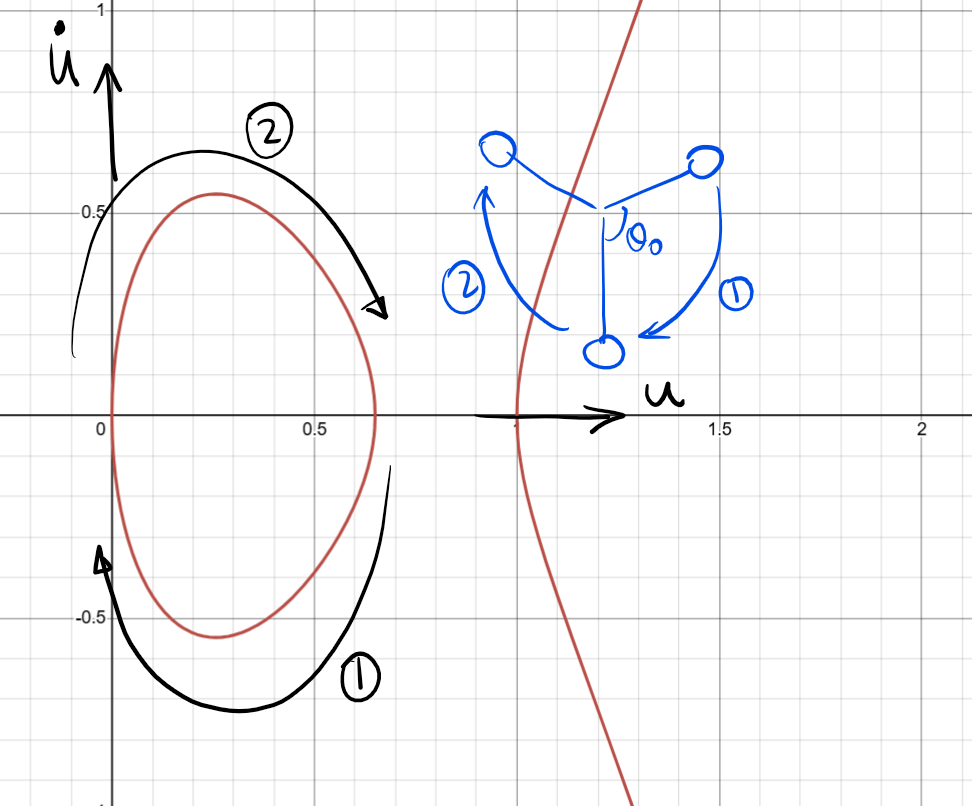
일반적인 진자의 주기 공식을 제1종 완전한 타원적분을 \eqref{eqn:complete-ellipk} 통해 쓰면 (Wikipedia, Eq. 3), $T=4\sqrt{L/g}K(\sqrt{\lambda})$와 같다. 따라서 주기 c는 $c=2K(\sqrt{\lambda})$로 나타난다. 여기에 더해 α를 구하는 역변환 공식에 의하면 $\alpha=K(\sqrt{1-\lambda})/K(\sqrt{\lambda})$이고.
따라서 다음과 같은 해를 찾는다.
단진자의 시간에 따른 높이. 단진자의 정규화된 에너지가 $\lambda=E/(2mgL)$이고 0<λ<1이라 할 때, 그리고 K가 제1종 완전한 타원적분 \eqref{eqn:complete-ellipk}이라 할 때 시간에 따른 높이 함수 u(t)는 다음 공식으로 나타난다.
\[u(t) = \frac{1+\lambda}{3} + \wp\left(t-t_0+\sqrt{-1}K(\sqrt{1-\lambda});2K(\sqrt{\lambda}),2\sqrt{-1}K(\sqrt{1-\lambda})\right).\]단, t0는 진자가 제일 낮은 지점에 있을 때의 시간이고, 위 식에서 단위 시간은 $\sqrt{L/g}$라 본다.
그러므로 따름정리에서 제시한 방법에 따라, $t\in[0,T]$가 균일한 확률로 뽑힌 시간이라 하면, $(u(t),\dot{u}(t))$는 자동으로 $(\wp(t+\frac12\omega_2;\Lambda),\wp’(t+\frac12\omega_2;\Lambda))$ 꼴 숫자를 균일한 확률로 뽑게 된다 (단, $\omega_2=\sqrt{-1}c\alpha$). 이로써 주 정리를 보였다.
수치 알고리즘
℘-함수 직접 계산하기
사실 stla의 구현을 참고해서 직접 ℘-함수값을 구해도 잘 샘플링이 되기는 한다. 몇 가지 디테일을 고려하고 나면 (가령 당 구현에서 p_weierstrass_from_w1_w2(w1,w2)라 구현한 함수는 실제로는 2*w1 및 2*w2 주기를 가진다) 다음과 같이 샘플링을 할 수 있다.
import numpy as np
from mpmath import ellipk # need to install mpmath
# import stla's p_weierstrass_from_w1_w2 as wp
"""" 1. 위의 링크를 따라 나오는 코드를 복사해서 별도 파일에 (예: foo.py) 저장 후,
from foo import p_weierstrass_from_w1_w2 as wp
를 적용하면 된다.
2. 다만 코드를 그대로 적용하기보다, p_weierstrass_from_w1_w2에
'derivatives=0' 옵션을 넣어 wp의 미분도 반환하게 조치한다.
아래 코드는 이 조치를 전제로 한 것이다."""
def legendre_data(param):
return ellipk(param), ellipk(1 - param)*1j, (1 + param)/3
def sampler(param_legendre, circle_data, switch_data):
"""
param_legendre = the lambda invariant of EC
circle_data = real-axis coordinate(s), in R/2Z
switch_data = vector of 0 and 1, of same length
with circle_data
"""
w1, w2, shift = legendre_data(param_legendre)
z_data = w1 * circle_data + w2 * switch_data
_P = wp(w1,w2)
_dP = wp(w1,w2,derivative=1)
return (np.array([shift + _P(j).real for j in z_data],dtype=np.float64),
np.array([_dP(j).real for j in z_data],dtype=np.float64))
이 구현 하에서 랜덤 샘플을 구한다면 다음과 같은 식일 것이다.
N = 3 # numer of samples
param_legendre = 4/5 # any number between 0 and 1
_c = np.random.uniform(0,2,N) # attention: 2
_s = np.random.choice([0,1],N)
x_coord, y_coord = sampler(param_legendre, _c, _s)
다만 실제로 이 코드를 실행하면 값이 튀는 경우가 많이 생긴다. 특히나 _s 쪽에서 0이 샘플링되고, _c 쪽에서 0이나 2 근처로 값이 잡힐 때 왕왕 발생하는 편이다. 이 때문에, 실제로는 사영좌표계를 생각해서 y_coord쪽의 값이 튈 경우 $[x:1:z]$ 꼴 점을 반환하도록 유도하는 편이 더 합리적인 편이다. 곧, 항등원 연결성분을 포함해서 샘플링을 할 경우 단순한 직교좌표계가 아닌 사영좌표계로 프레임을 짜고 샘플링을 하는 편이 수치적으로 안정한 결과를 준다.
Naïve한 Euler 수치해
앞선 글의 주제를 생각하면 그저 ℘-함수를 직접 계산하는 게 더 나을 수도 있다는 관점에 좀 당혹할 수 있겠다. 이는 naïve한 Euler 방법이 왕왕 이상한 그림을 그리기 때문이다. 다음 코드 예시를 가지고 얘기해 보자.
import numpy as np
from mpmath import ellipk
import matplotlib.pyplot as plt
# import stla's p_weierstrass_from_w1_w2 as wp
""" 비교용으로 타원곡선을 plot하기 위한 import로,
실제로는 필요하지 않다. """
def comparison_curve(param_legendre, len = 1000):
period = float(ellipk(param_legendre) * 3)
t = np.linspace(0,period,num=len)
w2 = ellipk(1 - param_legendre)*1j
_P = wp(w1,w2)
_dP = wp(w1,w2,derivative=1)
shift = (1 + param_legendre)/3
return np.array([_shift + _P(j+w2).real for j in t],dtype=np.float64), \
np.array([_dP(j+w2).real for j in t],dtype=np.float64)
def euler(x,y,dt):
return x+y*dt, y-np.sin(x)*dt
def euler_naive(param_legendre, len = 1000):
X = [np.arccos(1-2*param_legendre)]
Y = [0]
dt = float(ellipk(param_legendre) * 10) / len # 10주기 관찰
for i in range(1,len):
x,y = euler(X[-1],Y[-1],dt)
X.append(x); Y.append(y)
return np.array(X), np.array(Y)
def comparison_euler_naive(param_legendre, len = 1000, comparison=True):
# 비교용 곡선
if(comparison):
U_real, dU_real = comparison_curve(param_legendre,1000)
plt.plot(U_real, dU_real, '-')
# 실제 수치해
X, Y = euler_naive(param_legendre,len)
U = (1 - np.cos(X))/2
dU = np.sin(X) * Y / 2
# plot, show
plt.plot(U, dU, '-')
plt.show()
이 경우 comparison 옵션을 키고, len=1000으로 잡고 param_legendre=.5로 잡으면 다음과 같은 그림을 본다.
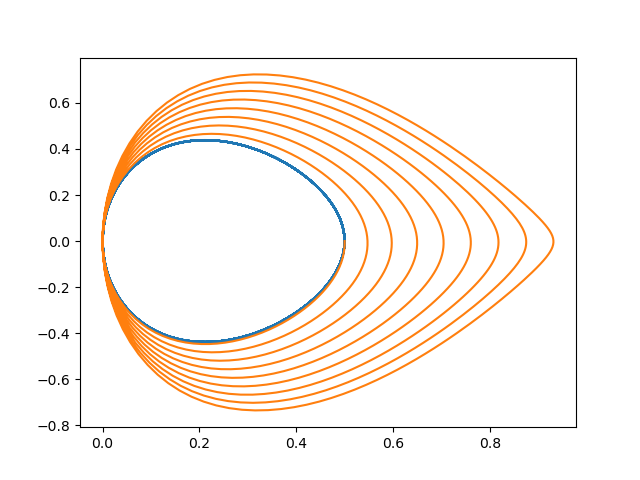
보다시피 타원곡선에서 점차 멀어지는 것을 볼 수 있다! 에너지에 대해 아무런 조치가 없기 때문인데, 사실 len=10000까지 늘려서 보면 “늘어는 나지만 쉽게 구분되지 않는” 선까지는 간다는 것을 볼 수 있다.
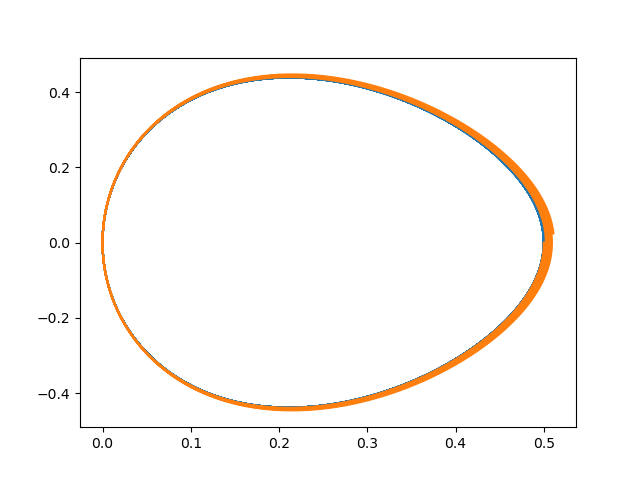
하지만 에너지 보정을 작정하고 하면 어떻게 될까?
에너지 보정 후 Euler 수치해
다음과 같이 Euler 수치해법을 수정해 보자. (comparison_curve 관련 함수는 삭제했다.)
import numpy as np
from mpmath import ellipk
import matplotlib.pyplot as plt
def euler_energy(x,y,dt,E):
x1 = x + y * dt
y11 = y - np.sin(x)*dt
y1 = np.abs(4*(E - .5) + 2 * np.cos(x1)) ** .5
if(y11 != 0.0): y1 *= y11 / np.abs(y11)
return x1, y1
def euler_with_energy(param_legendre, len = 1000):
X = [np.arccos(1-2*param_legendre)]
Y = [0]
dt = float(ellipk(param_legendre) * 10) / len # 10주기 관찰
for i in range(1,len):
x,y = euler_energy(X[-1],Y[-1],dt,param_legendre)
X.append(x); Y.append(y)
return np.array(X), np.array(Y)
def comparison_euler_energy(param_legendre, len = 1000):
# 실제 수치해
X, Y = euler_with_energy(param_legendre,len)
U = (1 - np.cos(X))/2
dU = np.sin(X) * Y / 2
# plot, show
plt.plot(U, dU, '-')
plt.show()
이 결과 보게 되는 그림은, (비교용 곡선과 그린 결과로) 타원곡선에 잘 붙어있는 그림이다.
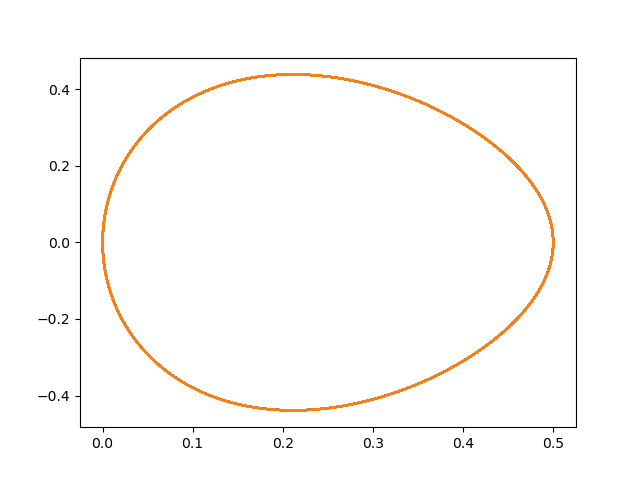
오른쪽 끝점에서 약간의 흔들림이 보이는데, 이는 y1 *= y11 / np.abs(y11)로 부호를 보정하는 과정에서 드러난 것으로 보인다.
실제로 이들이 잘 샘플링을 하는지 알아보려면, wp 함수로 샘플링한 것과 (U,dU)로 샘플링한 것에 대해서 몇 가지 평균값을 알아보면 되는 문제다. 가령, sum(U*U)/len(U) 등을 통해서 $\mathbb{E}[x^2]$ 값을 비교해 보는 식으로. 그 경우 의외로 둘의 값이 잘 맞아 떨어지는 것 또한 볼 수 있다.
Update Log
- 251106: Created
- 251121: 수치해 관련 절 추가