개평법
Published:
전통적인 산술로 2차방정식의 수치해를 구하는 방법에 대한 소개 및 여기서 도출되는 몇 가지 ‘숫자 놀이’에 대한 글.
머릿말
조선조 수학의 양상에 대해서, 내가 아는 몇 안 되는 지식은 이런 것이었다.
- 주변 국가와 (즉, 중·일과) 다르게, 주판 대신 산가지를 끝까지 써 왔다.
- 산가지의 자유도 자체는 주판보다는 높은 편이라, 작정하면 10차방정식같은 것도 풀 수 있었다고.
물론 역사적으로 깊이있게 들어가면 안 그래도 복잡한 동아시아 역사에 대한 더 깊은 이해가 필요할 수 있고, 나 자신은 어디까지나 (내가 공부한) 수학만 자신있게 말할 수 있는 입장이다 보니, 잘 해야 저 산가지를 가지고 구체적으로 뭘 했는가?에 대한 질문 정도에나 관심을 기울이게 되었다. 다행히 간단한 검색으로 홍주희 2008와 같이 쉽게 설명한 자료를 찾을 수 있었다.
다만 위의 논문은 18세기 이후의 조선조 수학에 대한 내용이라, 혹여 이런 방정식에 대한 기술이 얼마나 오래 전부터 있었는지에 대한 궁금함은 별도로 남게 되었다. 일례로 양휘산법과 같은 교과서는 송조에 편찬된 책이니만큼, 한반도에서는 고려에서 조선 초기까지 영향력 있는 책이었던 것으로 보인다. 우연히 현 소속교 도서관에 양휘산법의 영역(英譯)과 해설을 담은 책 Lam 1977이 있어, 적어도 해당 시대의 방정식 풀이에 대한 내용까지는 확인할 수 있었다.
이들 문헌에서 드러나는 방정식 해법을 현대적인 언어로 풀어 쓰면 ‘다항함수의 테일러 전개의 응용’으로 요약할 수 있다. 물론 그렇다고 거기서 미적분학의 씨앗이 있었다고 보기에는 비약이 심하나, (오히려 조립제법으로 ‘테일러 계수’를 얻었기 때문에 미분 개념 도입의 저항 요인만 있지 않았을까 싶다) 놀랍게도 현대의 초등 수학인 장제법長除法/긴 나눗셈/세로 나눗셈의 이론적인 근간이 이런 기법에 놓여 있기는 하다.
다항방정식의 수치해
상술한 문헌에서 나타나는 ‘방정식의 해’는 (정수로 정확히 떨어지도록 설계된 교과서 속 연습문제를 제외하면) 근호 등을 써서 내린 답이 아니라 수치해를 말한다. 따라서 ‘방정식의 풀이’라는 테크닉 또한 해의 수치해를 계산하는 데에 초점이 가 있다.
현대적인 미적분학 수업을 기억한다면, Newton’s method가 개중에 제일 쉽고 빠른 방법이라는 이해가 있을 것이다. 다만 Newton’s method는 참 해와의 거리의 estimate에 대해서는 탁월한 정보를 주지만, ‘이 결과가 소수점 아래 어디까지 믿을만한 결과인가?’ 라는 질문에 대해서는 쉬운 답을 주는 것 같지는 않다. (혹여 이러한 의문이 부적절한 것이면 알려주시기 바랍니다.)
반면 전통적인 ‘방정식의 풀이’는 비록 느릴지라도 소수점 아래 얼마까지 믿을 만한 해를 만들어낸다는 특징이 있다. 다음 일례를 보자.
예: 2의 제곱근
방정식 $x^2=2$를 생각하자. 기호로는 $x=\pm\sqrt{2}$를 답으로 제시할 수 있지만, 이 중 $x=\sqrt{2}$ 근을 수치해로 구한다고 생각해 보자. 일련의 과정을 묘사하고자, 함수 $f_0(x)=x^2-2$를 정의한다.
먼저 $\sqrt{2}$를 대략 추산할 양수를 잡자. 대개 원하는 숫자의 제일 큰 자리수를 여기서 쓸 수 있다. 이 경우 $x_0=1$을 시작점으로 잡는다. 좀 더 큰 숫자의 경우, 가령 $\sqrt{130}$와 같은 경우 시작점을 10으로 잡는다던가 할 수 있겠다.
이제 $1<\sqrt{2}<2$가 $1<2<4$에서 따르므로, $x_0=1$ 이후 소수점 자리수를 찾아보면 된다. 이에 참 해를 $\sqrt{2}=1+\frac{1}{10}t$로 쓰고, $t$에 대한 방정식을 다음과 같이 구한다.
\[f_0(1+\frac{t}{10}) = (1+\frac{t}{10})^2-2 \\ = \frac{t^2}{100}+\frac{2t}{10}-1=0.\]양변에 100을 곱하고 정리하면, $f_1(t) = t^2 + 20t - 100$을 안다. 즉, 새 방정식으로 $t^2+20t = 100$을 풀게 된 것이다. 이제 $t=0,1,2,\ldots,9$를 대입해 보면, $t=4$와 $t=5$에서 $f_1(4)<0<f_1(5)$를 알 수 있다. 이에 $x_1=4$라 두어 전개를 이어갈 수 있다. 곧, $t=4+\frac1{10}t’$라 잡고 (달리 이르면 $\sqrt{2}=1.4+\frac1{100}t’$라 두는 꼴이다)
\[f_1(4+\frac1{10}t') = (4+\frac{t'}{10})^2+20(4+\frac{t'}{10})-100 \\ =\ldots=\frac1{100}((t')^2+280t'-400)=0\]로 새 보조함수 $f_2(t’)=(t’)^2+280t’-400$ 및 방정식 $f_2(t’)=0$을 얻고… 하는 과정을 반복한다.
여기서 $f_0\to f_1\to f_2\to\ldots$로 전개하는 과정은 테일러 전개로 생각할 수 있다. 곧,
\[f_1(t) = 100\cdot f_0(1+\frac1{10}t) \\ = 100 f_0(1) + 10 f_0'(1)\cdot t + \frac{f_0''(1)}{2}t^2,\] \[f_2(t') = 100\cdot f_1(4+\frac1{10}t') \\ = 100 f_1(4) + 10f_1'(4)\cdot t' + \frac{f_1''(4)}{2}(t')^2\]와 같이 계산하는 꼴이다. (실제로 $100 f_0(1) = -100$, $10f_0’(1) = 20$, $100 f_1(4) = -400$, $10f_1’(4)=280$ 모두 참이다.) 게다가 주어진 다항함수가 monic이기에, 2차항 계수 $\frac12 f_i’’(\ast)$는 항상 1로 고정되어, 결국 다음 알고리즘을 따르게 된다.
- 제일 높은 자리수를 추산하여, $\sqrt{2} = 1 + \frac1{10}t$로 목표를 바꾼다.
- 주어진 방정식 $f_0(x)=0$에서 먼저 단계의 자리수 1을 반영해, 다음 방정식 $f_1(t)=100 f_0(1) + 10f_0’(1)\cdot t + t^2$을 얻는다.
- 반복해서, 주어진 방정식 $f_k(t)=0$에서 $t=q+\frac1{10}t’$로 두면, (단 $q=0,1,2,\ldots,9$ 중 하나) 다음 방정식 $f_{k+1}(t’)=100f_k(q)+10f_k’(q)\cdot t’ + (t’)^2$를 얻는다.
Remark. 위에서는 테일러 전개로 묘사하기는 했지만, 전통적인 관점에 더 어울리는 방식은 아무래도 조립제법일 것이다. 곧, $f_{k+1}(t')=100 f_k(q+\frac1{10}t')$를 변형해 얻는
\[f_{k+1}(t') = 100\cdot\underbrace{\frac{f_k(q+\frac1{10}t') - f_k(q)}{\frac1{10}t'}}_{(\ast)}\cdot \frac1{10}t' + f_k(q)\] 에서 몫 부분 $(\ast)$을 조립제법으로 계산하는 식으로도 이해할 수 있다. (이 관점은 홍주희 2008의 II.E절에서 따른 것이다.)
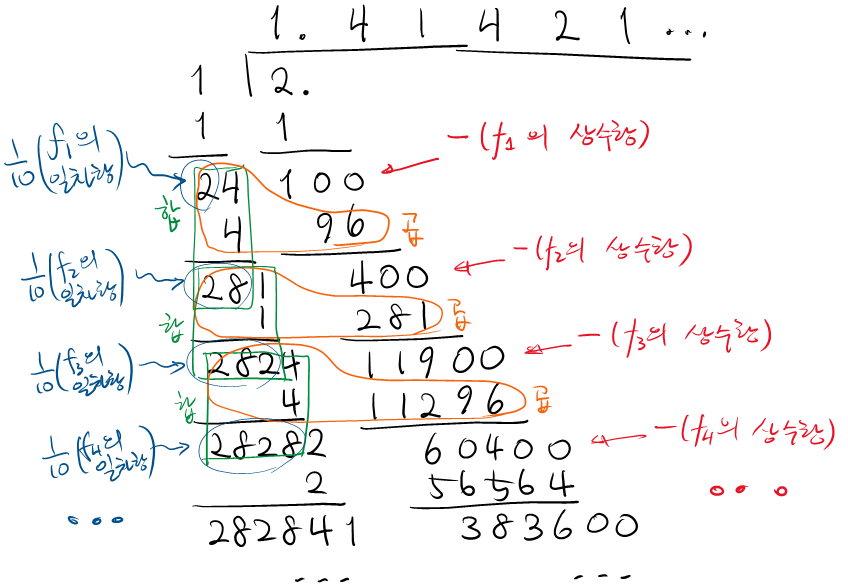
말마따나 복잡하지만, 이 알고리즘을 반복하다 보면 다음 데이터를 얻는다.
| $k$ | 자릿수 | $f_k$의 상수항 | $f_k$의 일차항 |
|---|---|---|---|
| 0 | 1 | -2 | 0 |
| 1 | 4 | -100 | 20 |
| 2 | 1 | -400 | 280 |
| 3 | 4 | -11900 | 2820 |
| 4 | 2 | -60400 | 28280 |
| 5 | 1 | -383600 | 282840 |
여전히 바로 직관적으로 와닿는 숫자들은 아니지만, 몇 가지 관찰할 점은 있다.
- $\sqrt{2} = 1.41421\ldots$는 계산기로 얻은 값과 합치한다.
- 가령 $k=3$까지 끊은 결과, $\sqrt{2}\approx 1.414$에서 1414를 20배하면 28280, 즉 $f_{k+1}$의 일차항 계수가 된다. 이러한 $k$단계까지 얻은 근삿값과 $f_{k+1}$의 일차항 계수 간 관계는 일정하게 성립한다.
- 또한 $f_{k+1}$의 상수항도 비슷하게 결정되는데, $f_k$의 상수항과 일차항을 각각 $c_k$, $l_k$라 쓰면 $c_{k+1} = 100\cdot(c_k + q(l_k + q))$로 나타난다. (가령 아래와 같은 식이다.)
- 사실 위 기호대로면 $l_{k+1}=10(l_k + 2q)$이기도 하다.
이 산법을 체계적인 세로셈으로 만든 방법이 개평법이다. (영문 위키, 일어 위키, 국문 자료 1, 국문 자료 2) 그림으로 그려내면 이런 식.
위의 계산을 응용하면 다음과 같은 계산도 가능하다.
- 방정식 $x^3-2=0$의 수치해를 위와 같이 구해서, $\sqrt[3]{2} = 1.2599210\ldots$를 손계산으로 구할 수 있다. 다만 이 경우 추적해야 하는 계수가 상수항, 1차항, 2차항으로 3개나 될 뿐더러, 1차항의 update 규칙이 워낙 복잡하다는 흠이 있다.
이 수치 알고리즘은 고차다항식으로 갈 수록 점차 더 쓰기 어려워지는 방법이기는 하다. - Nonarchimedean field가 이러한 수치 기법과 매우 친한 편이다. 가령 위의 개평법을 약간 응용해서, 7진수체 $\mathbb{Q}_7$에서 $\sqrt{2}$를 계산하는 등의 시도를 할 수 있다. 다만 다음 이유로 이러한 시도가 ‘숫자 놀이’의 선을 넘기는 힘든 것 같다.
- 자리수를 합하고 곱하는 과정을 7진법으로 해야 해서, 중간과정의 점검이 매우 혼란하다.
- 번듯이 Hensel’s Lemma라는 대안이 있는 상황이기도 하다.
예: 나눗셈
앞서서는 바로 고차방정식으로 넘어가느라 워낙 힘든 수학이 한꺼번에 쏟아졌지만, 사실 1차방정식에 대해서도 유의미한 결과를 주는 방법이기도 하다. 다음 방정식을 생각하자.
\[7x=10.\]이 방정식의 수치해를 구한다고 생각하자. 그러면 해 $x=10/7$의 정수부는 1이다. (10을 7로 나눈 몫과 나머지를 생각해 보면 된다.) 이후 해의 ‘다음 자리수’를 구하는 일차방정식을 쓰고, 이를 반복하면 다음과 같다.
| 단계 | 지금 방정식 | 근사해 | 다음 미지수 | 다음 방정식 | $10/7=\ldots$ |
|---|---|---|---|---|---|
| 0 | $7x=10$ | $x\approx 1$ | $x=1+0.1t$ | $7t=30$ | $1.\ldots$ |
| 1 | $7x=30$ | $x\approx 4$ | $x=4+0.1t$ | $7t=20$ | $1.4\ldots$ |
| 2 | $7x=20$ | $x\approx 2$ | $x=2+0.1t$ | $7t=60$ | $1.42\ldots$ |
| 3 | $7x=60$ | $x\approx 8$ | $x=8+0.1t$ | $7t=40$ | $1.428\ldots$ |
| 4 | $7x=40$ | $x\approx 5$ | $x=5+0.1t$ | $7t=50$ | $1.4285\ldots$ |
| 5 | $7x=50$ | $x\approx 7$ | $x=7+0.1t$ | $7t=10$ | $1.42857\ldots$ |
| 6 | $7x=10$ | $x\approx 1$ | $x=1+0.1t$ | $7t=30$ | $1.428571\ldots$ |
이로써 (잘 알려져 있듯) 어느 시점부터는 ‘다음 방정식’이 반복하게 되어, 순환하는 무한소수를 답으로 얻는다. 나아가 이 일련의 계산과 다음의 긴 나눗셈 사이 관계도 그리 어렵지 않을 터이다.
\[\begin{array}{r} 1.42857\phantom{9)} \\ 7{\overline{\smash{\big)}\,10.\phantom{999999)}}} \\ \underline{7\phantom{9}}\phantom{.99999)}\\ 3\phantom{.}0\phantom{99999)}\\ \underline{2\phantom{.}8}\phantom{99999)}\\ 20\phantom{9999)}\\ \underline{14\phantom{9}}\phantom{999)}\\ 60\phantom{999)}\\ \underline{56\phantom{9}}\phantom{99)}\\ 40\phantom{99)}\\ \underline{35\phantom{9}}\phantom{9)}\\ 50\phantom{9)}\\ \underline{49\phantom{9}}\phantom{)}\\ 10\phantom{)} \end{array}\]방정方程의 기하학
앞선 방정식 풀이는 순수하게 대수적 언어만 가지고 묘사하기는 했지만, (양휘산법 등에 나타난) 방정식을 풀어야 하는 상황이나 그 풀이에 대한 이해는 꽤나 기하학을 염두에 둔 것으로 보인다. 다음 문제를 생각해 보자.
문제. 직사각형 밭의 두 변의 차이가 12보이고, 면적이 864제곱보이다. 밭의 두 변을 구하라.
(풀이 1) 두 변 중 짧은 쪽을 $x$라 쓰면, 밭의 면적은 한 변이 $x$인 정사각형 하나와, 두 변이 각각 $x$와 12인 직사각형 하나로 쪼갤 수 있다. (아래 그림의 왼쪽.)
이제 (약간의 시행착오를 통해) $x>20$은 되어야 한다는 것을 안다. (만약 $x=20$이라면 면적이 $x^2+12x=640$밖에 안 되는 까닭이다.) 달리 말하면, 이 밭에서 $x=20$에 해당하는 면적 정도는 파 내도 $864-640=224$만큼의 면적은 어쨌건 남는단 말이다. (아래 그림의 오른쪽.)

이 때 남는 길이 $y=x-20$에 의한 면적은 $20\cdot y + y^2 + y\cdot 20 + y\cdot 12 = y^2+52y=224$로 나타나고, 다시 (시행착오 후) $y=4$에서 수가 맞아 떨어짐을 안다. 따라서 $x=24$, $x+12=36$이 두 변이 된다. $\square$
보면, 이 ‘기하학적 방법’은 $x^2+ax=b$ 꼴 (단 $a,b\geq 0$) 방정식이라면 그려 볼 법한 그림으로 풀이를 해설하고 있다. 이것을 다시 앞에서의 ‘순수 대수적인’ 방법으로 구해보면 다음과 같다.
(풀이 2) 다항식 $f(x) = x(x+12)-864$를 생각하자. (따라서 문제 상황은 $f$의 (양의) 영점을 찾는 것이다.) 이 때 $f(20)<0$이므로 $x=20+y$로 해를 근사하면,
\[f(20+y) = y^2 + 52y - 224 = 0\]을 찾는 문제가 된다. 여기서 $y=4+0.1z$로 또 근사하면, $100\cdot f(20+(4+0.1z))=600z+z^2$인 즉, $z=0$이 하나의 근이 되어 $x=24$ 답을 얻는다. $\square$
앞서의 ‘자리수 하나씩 찾기’ 기법을 다시 쓴 건데, 보다시피 기하학적인 방법에서 나타난 숫자들을 대수적으로 되찾은 것 이상의 내용이 보이지 않는다.
2의 제곱근
되려, 앞서 소개한 $\sqrt{2}$을 개평법이 아닌 그림으로 산출하는 방법을 얻은 것일 수도 있겠다. (다음 그림 참고)

즉, 한 변이 $\sqrt{2}$인 정사각형을 생각하고, 여기서 변을 1, 0.4, 0.01, 0.004, … 씩 파 내려가서 나오는 그림을 생각하는 것이다. 가령 그림처럼 1, 0.4의 두 단계를 파 내려가면 남은 면적 $2.8z+z^2 = 0.04$를 얻는데, 이는 앞서 $f_2(x)=x^2+280x-400$과 통하는 면이 보이는 수식이다. (사실 ‘남은 면적’ 공식이 $f_2(100z)=0$ 그 자체이다.)
확장성
개평법을 재발견하는 기능 외에도, 위 기하학적 논거는 개평법이 $x^2+ax=b$, $a,b\geq 0$ 꼴의 방정식의 양수해를 구하는 데에도 쓰일 수 있다는 암시를 준다. 미지의 길이 $x$의 근사해만큼 직사각형+정사각형 그림을 ‘파 내고’ 남는 길이와 면적을 산출하는 식으로 근사할 여지를 남기는 것이다.
좀 더 명시적으로 수치해 구하기를 묘사하면 다음과 같다.
- 재귀적으로, $k\geq 0$이라 하고, monic 2차식 $f_k(x)=x^2+a_kx-b_k$에 양수 근 $x$가 있고 $x_k<x$가 적당한 근사해라 하자.
- 그러면 오차항 $0.1t = x-x_k$라 둘 때 $f_{k+1}(t)(=100 f_k(x_k+0.1t))=t^2+a_{k+1}t-b_{k+1}$는 다음과 같이 정해진다.
- $b_{k+1} = 100\cdot(b_k-x_k(a_k+x_k))$, $a_{k+1}=10\cdot(a_k+2x_k)$.
예: 황금비
황금비를 손계산으로 구한다고 하면, 먼저 떠올릴 만한 방법으로는 $\sqrt{5}$를 개평법으로 구하고 그걸 근거로 $\phi=(1+\sqrt{5})/2$를 계산하거나, 조금 더 정교하게 $\sqrt{5}/2 = \sqrt{1.25}$를 개평법으로 계산해서 0.5를 더하는 방법 등을 생각할 수 있을 것이다.
그러나 앞서 묘사한 2차방정식 수치해 구하기를 생각하면, 그저 그런 절차 없이 바로 황금비를 계산할 수 있다. 이에 $f_0(x) = x^2-x-1$라 두자.
물론 $f_0(x)=0$ 방정식에 기하학적인 의미를 두기는 쉽지 않다. 정사각형에 적당한 직사각형 면적을 빼야 한다는 말인데, 그 경우 길이를 파내는 과정이나 남는 면적을 산출하는 과정 등이 이해가 쉽지는 않기 때문이다. 다만, 황금비 $\phi=1.618\ldots$로 시작한다는 것은 알고 있으니, $x_0=1$이라 두고 과정을 이어 갈 수는 있다.
이 경우 $f_1(t) = 100 f_0(1+0.1t) = t^2+10t-100$로 다음 오차항의 방정식을 얻고, 이하 계산을 이어갈 수 있다. 다만 첫 단계에 대해 재밌는 점이 있어, 이 점을 ‘개평법’처럼 써서 나타내 보도록 한다.
\[\begin{array}{rl} 1.\phantom{999)}\\ -1{\overline{\smash{\big)}\phantom{999}\,1.\phantom{999)}}} \\ 1\;\;\;\;\! -1\phantom{1.99)} & (\ast 1)\\ \underline{1}\phantom{9}\;\;\;\;\! \underline{\phantom{-}1}\phantom{1.99)} & (\ast 2) \\ 1\;\;\;\;\!\phantom{-}1\phantom{1.99)} \end{array}\]처음 방정식이 $x^2-x=1$ 꼴이므로, 이 ‘변종 개평법’의 첫 줄은 일차항 $-1$과 (음의) 상수항 1을 나열한다. 그 다음 줄 $(\ast 1)$은 (i) 제일 왼쪽에 첫 자리수 1을 적고, (ii) 상수항에 $(-1)\times 1$을 뺀다. 그 다음 줄 $(\ast 2)$는 (i) 제일 왼쪽에 첫 자리수 1을 반복해 적고, (ii) 상수항에 $1\times 1$을 뺀다. 이상으로
- 줄 $(\ast 1)$에서는 $a_k$에서 $x_k$를 더하고, $b_k$에서 $x_ka_k$를 빼라는 말이고,
- 줄 $(\ast 2)$에서는 $a_k$에 $x_k$를 더하고, $b_k$에서 $x_k^2$를 빼라는 말이다.
이에 종합하면 $a_k+2x_k=\frac1{10}a_{k+1}$ 및 $b_k-x_k(a_k+x_k)=\frac1{100}b_k$를 구하는 셈이다. 해서
- 왼쪽 열에서는 $(-1)+1+1=1$이 줄 아래에 적히고,
- 오른쪽 열에서는 $1-(-1)\cdot 1-1\cdot 1 = 1$이 줄 아래에 적힌다.
이후 적당히 자리수를 shift하고 개평법을 쭉 전개해 가면 다음과 같다.
\[\begin{array}{r} 1.\phantom{9}6\phantom{9}1\phantom{9}8\phantom{9}0\phantom{9}3\phantom{9}3\phantom{9}9\phantom{9}8\phantom{)}\\ -1{\overline{\smash{\big)}\phantom{999}\,1.\phantom{9999999999999999)}}} \\ 1\;\;\;\;\! -1\phantom{1.999999999999999)}\\ \underline{1\phantom{9}}\;\;\;\;\! \underline{\phantom{-}1}\phantom{1.999999999999999)}\\ 16\phantom{9-}1\phantom{.}00\phantom{99999999999999)} \\ \underline{\phantom{9}6}\phantom{9-}\underline{\phantom{9.}96\phantom{99}}\phantom{999999999999)} \\ 221\phantom{-.99}400\phantom{999999999999)} \\ \underline{\phantom{99}1}\phantom{-.99}\underline{221\phantom{99}}\phantom{9999999999)} \\ 2228\phantom{-.9}17900\phantom{9999999999)} \\ \underline{\phantom{999}8}\phantom{-.9}\underline{17824\phantom{99}}\phantom{99999999)} \\ 22360\phantom{-.999}7600\phantom{99999999)} \\ \underline{\phantom{9999}0}\phantom{-.999}\underline{\phantom{999}0\phantom{99}}\phantom{999999)} \\ 223603\phantom{-.99}760000\phantom{999999)}\\ \underline{\phantom{99999}3}\phantom{-.99}\underline{670809\phantom{99}}\phantom{9999)} \\ 2236063\phantom{-.99}8919100\phantom{9999)} \\ \underline{\phantom{999999}3}\phantom{-.99}\underline{6708189\phantom{99}} \phantom{99)}\\ 22360669\phantom{-.9}221091100\phantom{99)} \\ \underline{\phantom{9999999}9}\phantom{-.9}\underline{201246021\phantom{99}}\phantom{)} \\ 223606788\phantom{-.9}1984507900\phantom{)} \\ \underline{\phantom{99999999}8}\phantom{-.9}\underline{1788854304}\phantom{)} \\ 223606796\phantom{-.99}195653596\phantom{)} \\ \ldots \end{array}\]한 가지 여기서 주의할 점이 있다면, 이제 왼편의 숫자와 $\phi=1.61803398\ldots$와 관계를 찾기가 더 힘들어졌다는 점이겠다. (사실 왼편의 숫자의 절반을 취하면 $\sqrt{1.25}=1.16803398\ldots$의 자리수가 나온다. 즉 앞서 이론 전개 이전에 제시한 ‘$\sqrt{1.25}$ 계산 후 0.5 더하기’가 위에서 실질적으로 진행 중인 작업인 셈이다.)