This series of posts is aimed to be a rudiment of the Berkovich line, a locally compact space that “fills up” a non-archimedean field $K$. This post continues from part 1.

Previously

• Fix a non-archimedean field $(K,\vert\cdot\vert_K)$ which is algebraically closed and Cauchy complete. Let $q>1$ be a number such that the valuation $v(\cdot)$ is evaluated $v(x)=-\log_q\vert x\vert_K$.
• Given a $K$-algebra $A$, its multiplicative seminorm is a $K$-algebra seminorm $\vert\cdot\vert\colon A\to[0,\infty)$ such that $\vert fg\vert=\vert f\vert\cdot\vert g\vert$ holds. The Berkovich spectrum $\widehat{A}$ collects all multiplicative seminorms of $A$.

More Multiplicative Seminorms of $K[T]$

We continue the discussions on the multiplicative seminorms of $K[T]$. Other than the evaluation seminorms $\vert f(T)\vert_a := \vert f(a)\vert$ (by $a\in K$), all such seminorms are multiplicative norms.

In the sequels, we assume that $\vert\cdot\vert_K$ is nondiscrete, in the sense that there exists $x\in K$ such that $\vert x\vert_K\neq 0,1$.

Ball norms

According to Berkovich classification theorem, the building blocks of such norms are the sup norms on the balls. To elaborate, we denote

for closed balls (unlike the usual metric space convention, indeed). As a side note, we remark some interesting facts about these.

Proposition 1. (1) Any point in a closed ball could be the center. (That is, for any $b\in B(a,r)$, $B(a,r)=B(b,r)$.)

(2) Any two closed balls in $K$ are either nested or disjoint. (That is, for any two balls $B(a,r)$ and $B(b,s)$, with $r\leq s$, either $B(a,r)\cap B(b,s)=\varnothing$ or $B(a,r)\subset B(b,s)$.)

(Proof) (2) comes from (1) because if $B(a,r)\cap B(b,s)\neq\varnothing$, then I can replace centers of both balls to the intersection point. (1) follows from $\vert x-b\vert_K\leq\max(\vert x-a\vert_K,\vert b-a\vert_K)\leq r$ whenever $x,b\in B(a,r)$, showing $B(b,r)\subset B(a,r)$. As $a\in B(b,r)$, we can argue symmetrically.

$\square$

Define the ball norm (on $B(a,r)$) as

Of course, this defines a $K$-algebra norm on $K[T]$, but it is nontrivial to see that this is a multiplicative norm. We state it as a

Theorem 2. For $f,g\in K[T]$, we have $\vert fg\vert_{B(a,r)}=\vert f\vert_{B(a,r)}\vert g\vert_{B(a,r)}$.

This result is based on the following Lemma.

Lemma 3. Write $f(T)\in K[T]$ as $f(T)=\sum_{i=0}^dc_i(T-a)^i$. Then we have

\begin{equation}\label{eqn:ball-norm-formula}\vert f(T)\vert_{B(a,r)} = \max\left(\vert c_i\vert_K\cdot r^i : 0\leq i\leq d\right).\end{equation}

(Proof) If $x\in B(a,r)$, then $\vert f(x)\vert_K = \vert\sum_{i=0}^dc_i(x-a)^i\vert_K\leq\max_{i=0}^d\vert c_i\vert_K\cdot\vert x-a\vert_K^i\leq\max_{i=0}^d\vert c_i\vert_K\cdot r^i$, so we have \(\vert f(T)\vert_{B(a,r)}\leq\max\{\vert c_i\vert_K\cdot r^i : 0\leq i\leq d\}\).

Because $r\mapsto\vert f(T)\vert_{B(a,r)}$ is an increasing function and \(r\mapsto\max\{\vert c_i\vert_K\cdot r^i : 0\leq i\leq d\}\) is a continuous function, it suffices to verify the equation \eqref{eqn:ball-norm-formula} for a dense set of $r\in[0,\infty)$. We need two ingredients to describe this dense set:

• Denote $\vert K^\times\vert$ for the possible nonzero norm values of $K$. (Even for \(K=\mathbb{C}_p\), this set is not equal to \(\mathbb{R}_{>0}=(0,\infty)\), but equals to $p^{\mathbb{Q}}$.) Let $x\in K^\times$ be such that $\vert x\vert_K=:s\neq 0,1$. Then as $x^{p/q}\in K^\times$ for any $p/q\in\mathbb{Q}$, it follows that $s^{\mathbb{Q}}\subset\vert K^\times\vert$. So $\vert K^\times\vert\subset(0,\infty)$ is dense.
• Denote \(S = \{r>0 : (\exists i,j)(i\neq j\text{ and }\vert c_i\vert_K\cdot r^i=\vert c_j\vert_K\cdot r^j)\}\). Then $S$ is a finite set.

We then show that for $r\in\vert K^\times\vert\setminus S$, we have \eqref{eqn:ball-norm-formula}. Because $r\in\vert K^\times\vert$, $r=\vert \epsilon\vert$ for some $\epsilon\in K$. As $r\notin S$, we have only one $0\leq i\leq d$ such that \(\vert c_i\epsilon^i\vert_K=\max\{\vert c_i\epsilon^i\vert_K : 0\leq i\leq d\}\). Thus the inequality

now becomes equality (by an axiom of nonarchimedean field norms). The equality \eqref{eqn:ball-norm-formula} follows.

$\square$

Corollary. For each polynomial $f(T)\in K[T]$ and $a\in K$, there is a finite set $S(f,a)\subset\vert K^\times\vert$ such that for each $r\in\vert K^\times\vert\setminus S(f,a)$, any $x\in K$ with $\vert x-a\vert_K=r$ has $\vert f(T)\vert_{B(a,r)}=\vert f(x)\vert_K$.

(Proof of Theorem 2.) Set $S=S(f,a)\cup S(g,a)\cup S(fg,a)$. Then $S$ is finite, and for each $r\in\vert K^\times\vert\setminus S$, we have

For other $r>0$, appeal to the continuity of $r\mapsto\vert f\vert_{B(a,r)}$, etc., and that $\vert K^\times\vert\setminus S\subset[0,\infty)$ is dense.

$\square$

Although the proof above is quite elementary, it is far from capturing the complete sense that the theorem encodes. We will return to this later (in the next post, with the concept of tropicalization.

Example. Previously we have defined a norm on $L=K(T)$ as follows. For $f\in K(T)$, write

\[f(T) = a\cdot\frac{(T-x_1)(T-x_2)\ldots(T-x_n)}{(T-y_1)(T-y_2)\ldots(T-y_m)},\]

and declare

\[\vert f(T)\vert_L = \vert a\vert\cdot\frac{\max(1,\vert x_1\vert)\cdot \max(1,\vert x_2\vert)\cdots\max(1,\vert x_n\vert)}{\max(1,\vert y_1\vert)\cdot\max(1,\vert y_2\vert)\cdots\max(1,\vert y_m\vert)}.\]

This norm is precisely the norm $\vert\cdot\vert_{B(0,1)}$ on $K[T]$ extended multiplicatively to $K(T)$. (Check: $\vert T-x\vert_{B(0,1)}=\max(\vert x\vert_K,1)$.) By this we have $\vert f+g\vert_L\leq\vert f\vert_L+\vert g\vert_L$, or even better, $\leq\max(\vert f\vert_L,\vert g\vert_L)$ (cf. Proposition 4).

Void intersection norms

Another class of norm rises from a nested family of balls in $K$, i.e.,

For $\mathbb{R}$ or $\mathbb{C}$, such a sequence admits the nonempty total intersection $\bigcap B:=\bigcap_n B(a_n,r_n)$. But in the nonarchimedean case, the intersection may be empty.

• Not all intersections are void for nonarchimedean cases, however. For instance, if the centers $(a_n)$ converge to $a$, then for $r=\inf_n r_n$, we have $\bigcap B=B(a,r)$.

Example. Let $K=\mathbb{C}_p$, for any prime $p$. Think of the balls

\[B_n:=B(p^{-1/2}+p^{-1/4}+\cdots+p^{-1/2^{n-1}},p^{1/2^n})\subset K.\]

One can then show that $B_{n+1}\subset B_n$ as follows. Let $a_n=p^{-1/2}+p^{-1/4}+\ldots+p^{-1/2^{n-1}}$, the center of the ball $B_n$. Then as $\vert a_{n+1}-a_n\vert_p=\vert p^{-1/2^n}\vert_p=p^{1/2^n}$, we have $a_{n+1}\in B_{n}\cap B_{n+1}$. As $p^{-1/2^{n+1}}<p^{-1/2^n}$, Proposition 1 applies.

However, if there were any point $x\in\bigcap_{n=1}^\infty B_n$, we must have $\vert a_{n+1}-a_n\vert_K\leq\vert x-a_{n+1}\vert_K+\vert x-a_n\vert_K<\frac12$ for $n$ big enough. This contradicts with $\vert a_{n+1}-a_n\vert_K=p^{-1/2^n}>1$.

Such a nested family of balls with void intersection defines a norm, in which I coin void intersection norms, defined as follows.

Indeed the limit on the right-hand side is always a decreasing limit, so the limit always exists. Multiplicative seminorm property trivially follows from those of ball norms on $B(a_n,r_n)$’s.

My understanding of this norm is that a nested family of balls with void intersection builds a “ghost ball” declared with a “ghost center $a=\lim_n a_n$” and a “ghost radius $r=\inf_nr_n$,” and declares the ball norm on that ball. If we think of the so-called ‘maximally complete extension’ (cf. Poonen 1993, Cor. 5.6) of $K$, then one can realize this “ghost ball” as a ball in the extension; the ball norm in the extension then coincides with the void intersection norm.

(Proof) Maximally complete fields admit nonempty intersections for any family of nested balls. Let $K\subset K’$ be an immediate maximally complete extension, and denote $B(a,r)$ and $B’(a,r)$ denote balls in $K$ and $K’$, respectively. Set the “ghost center” $x\in\bigcap B(a_n,r_n)$ (in $K’$) and “ghost radius” $r=\inf r_n$. Then for any $f\in K[T]$, using Lemma 3,

Here the equality $\vert f\vert_{B’(a,r)}=\vert f\vert_{B(a,r)}$ is also a result of Lemma 3. So void intersection norm is the ball norm in disguise. $\square$

Berkovich Classification Theorem

By far we have discovered the following types of multiplicative seminorms on $K[T]$:

• Evaluation seminorms (i.e., $\vert f\vert_a:=\vert f(a)\vert_K$),
• Ball norms with rational radii (i.e., $\vert\cdot\vert_{B(a,r)}$ with $r\in\vert K^\times\vert$),
• Ball norms with irrational radii (i.e., $\vert\cdot\vert_{B(a,r)}$ with $r\notin\vert K^\times\vert$), and
• Void intersection norms.

Berkovich Classification Theorem. The above four types of seminorms are all you get as multiplicative seminorms of $K[T]$, given a nonarchimedean, algebraically closed, Cauchy complete field $K$.

A proof can be found in (Berkovich 1990, Sec. 1.4.4), in which I brief as follows. Given a multiplicative seminorm $\vert\cdot\vert_x$, think of the family of balls \(B_x=\{B(a,\vert T-a\vert_x) : a\in K\}\). This is a nested family, as followed by

Proposition 4. For any multiplicative seminorm $\vert\cdot\vert$ on a $K$-algebra $A$, where $(K,\vert\cdot\vert_K)$ is a nonarchimedean field, then the seminorm is nonarchimedean. That is, we have $\vert f+g\vert\leq\max(\vert f\vert,\vert g\vert)$ for any $f,g\in A$.

(Proof: Baker & Rumely 2010, Lem 1.1(C)) The punchline is, (1) for any integer $k\in\mathbb{Z}$, $\vert k\vert_K\leq 1$, and thus (2) by binomial theorem, $\vert f+g\vert^n\leq\sum_0^n\vert\binom{n}{j}\vert_K\cdot\vert f\vert^j\vert g\vert^{n-j}\lesssim n\cdot\max(\vert f\vert,\vert g\vert)^n$. Take the $n$-th root for (2) and send $n\to\infty$ to finish.

$\square$

So by Proposition 4, we have $\vert a-b\vert_K=\vert a-b\vert_x\leq\max(\vert T-a\vert_x,\vert T-b\vert_x)$. Hence if $\vert T-a\vert_x\leq\vert T-b\vert_x$, then balls $B(a,\vert T-a\vert_x)$ and $B(b,\vert T-b\vert_x)$ intersects at $a$, thus nested by Proposition 1. The intersection $\bigcap B_x$ is either empty (gives a void intersection norm) or nonempty (gives an evaluation or ball norm), and the classification follows.

Berkovich Line

Definition. The Berkovich line $(\mathbb{A}^1_K)^{an}$ is the Berkovich spectrum of $K[T]$. That is, it is the space of multiplicative seminorms of $K[T]$.

Elements of the Berkovich line are classified as in Berkovich classification theorem. Furthermore, the topology of this space is described in the following equivalent ways:

• (By subbasic open sets) For each polynomial $f\in K[T]$ and an open interval $(\alpha,\beta)\subset\mathbb{R}$, define subbasic open sets of $(\mathbb{A}^1_K)^{an}$ as

• (By subspace topology) Think of the natural embedding \((\mathbb{A}^1_K)^{an}\subset\prod_{f\in K[T]}[0,\infty)\), described below. Then \((\mathbb{A}^1_K)^{an}\) inherits subspace topology from the product space.

It is a simple exercise to actually show that evaluation seminorms give a topological embedding $K\subset(\mathbb{A}^1_K)^{an}$. Furthermore,

Proposition 5. Evaluation seminorms $K\subset(\mathbb{A}^1_K)^{an}$ are dense.

(Proof) This follows from a general fact (cf. Berkovich 1990, Proposition 2.1.15) about Berkovich spectra, that Gel’fand spectrum is dense in the Berkovich spectrum. The proof I know depends on the theory of affinoid spaces. So instead I present a more elementary proof tailored for the Berkovich line.

By definition, any void intersection norm can be approximated by ball norms. By Lemma 3, any ball norm with irrational radii can be approximated by those with rational radii.

Finally, suppose we fix a neighborhood $\bigcap_{i=1}^kU(f_i,(\alpha_i,\beta_i))$ of a rational ball norm $\vert\cdot\vert_{B(a,r)}$. By the Corollary to Lem. 3, except for finite exceptional $r$’s, any $x\in K$ with $\vert x-a\vert_K=r$ has $\vert f_i\vert_{B(a,r)}=\vert f_i\vert_x$. So $\vert\cdot\vert_{B(a,r)}$ is approximated by $\vert\cdot\vert_x$, for some $x\in K$. (For exceptional $r$, approximate to a non-exceptional $r’$ and continue.)

$\square$

In fact, evaluation seminorms can also be approximated by a ball norm: it holds that $\vert\cdot\vert_a\approx\vert\cdot\vert_{B(a,\epsilon)}$, depending on the neighborhood specified. So ball norms with rational radii are also dense in $(\mathbb{A}^1_K)^{an}$.

Visualization

Now we have a complete understanding of the Berkovich line $(\mathbb{A}^1_K)^{an}$ in an elementwise fashion. However, some simple topological observations admits us to visualize this ‘line’ as a tree with infinite valence. We list the observations below, and aim to sketch the Berkovich line visually.

Suppose $x=\vert\cdot\vert_{B(a,r)}$ and $y=\vert\cdot\vert_{B(b,s)}$ in $(\mathbb{A}^1_K)^{an}$, where we admit $r=0$ or $s=0$. Thus $x,y$ represents a generic evaluation seminorm or ball norm. There we have a dichotomy:

1. $B(a,r)\subset B(b,s)$.

In that case, we have $B(b,s)=B(a,s)$. Then one can build a (unique) path $x\to y$ by increasing the radii $r\to s$.

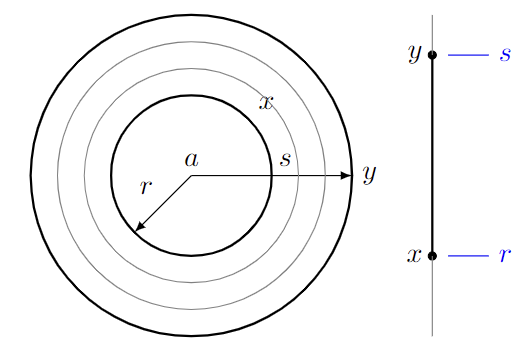
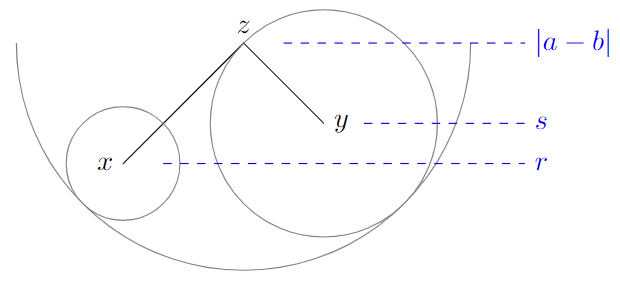
1. $B(a,r)$ and $B(b,s)$ are disjoint.

In that case, we have $r,s<\vert a-b\vert$. Let $z=B(a,\vert a-b\vert)=B(b,\vert a-b\vert)$. Then one can build a (unique) path $x\to y$ by first going $x\to z$ by increasing the radii, then $z\to y$ by decreasing the radii.

If we continue this sketch for a variety of balls $B(a,r)$’s, we get the following picture. (Figure source: M. Baker 2007, Figure 1.) In the figure, $\zeta_{\mathrm{Gauss}}:=\vert\cdot\vert_{B(0,1)}$.

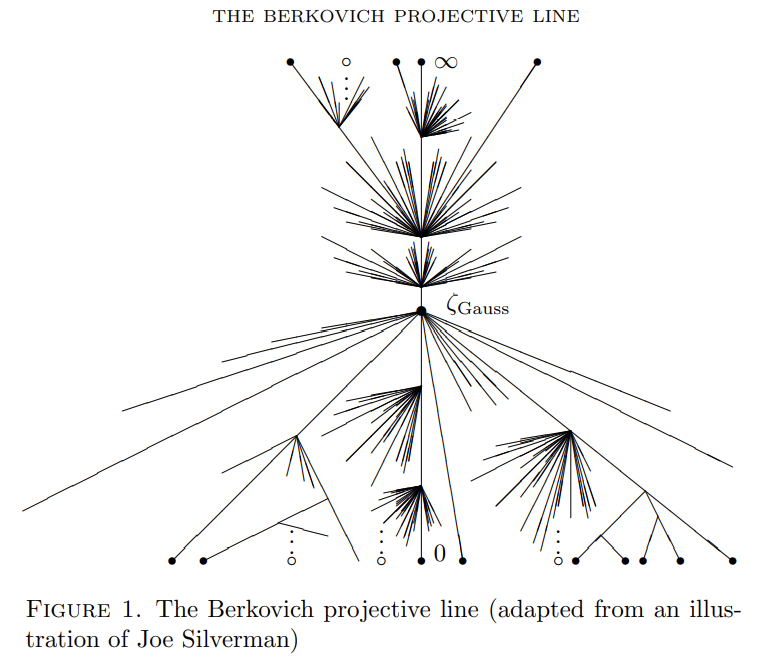
We observe many branches emitting from branch points, as well as a line that buds upwards from them. The lines bijectively correspond to $\mathbb{P}^1(\kappa)$, where $\kappa$ is the residue field of $K$: $\kappa:=\mathcal{O}_K/\mathfrak{m}_K$ where

We further observe:

• The points $a\in K$ lie at “endpoints.”
• The branching only occurs at balls with rational radii. At irrational radii, we can only go up/down.
• Void intersection norms appear along some of the branches that do not go all the way to endpoints, but rather ‘cauterized off’ earlier.

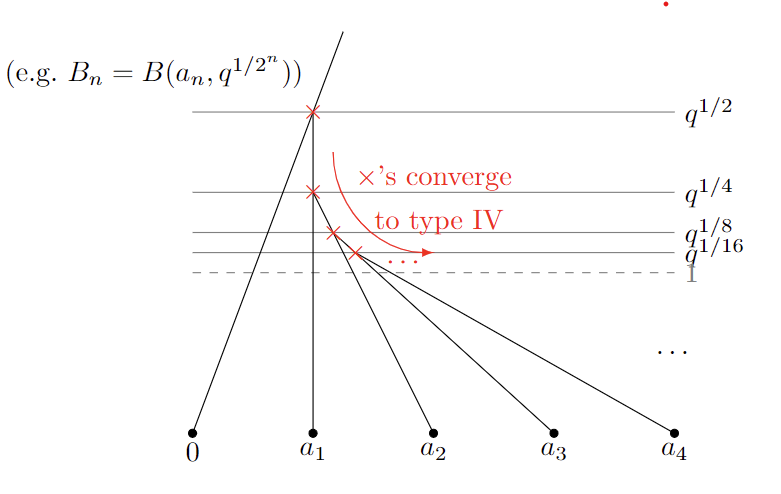
• The balls $B(0,r)$’s are vertically connected from $\zeta_{\mathrm{Gauss}}$. Through these balls, we can access some endpoints $a\in K$ with $v(a)<0$. Furthermore, sending $r\to\infty$, we reach to the ‘point at infinity,’ $\infty$.

Next

Next, we introduce the concept of tropicalization of a polynomial or a variety over a nonarchimedean field $K$ (although the notion may apply to archimedean fields as well). Based on that, one can introduce Payne’s tropicalization theorem of Berkovich spectra, and even show it for Berkovich lines. Link to part 3

Update Log

• 220727: Created
• 220812: Remedying some nonsense sentences
• 220914: Appended a proof of some claim on void intersection norm; for my reference