Maxwell의 도깨비, Landauer principle 등을 보고 떠오른 잡상雜想.

Maxwell의 도깨비

Maxwell의 도깨비, 혹은 Maxwell의 악마는 열역학, 특히 열역학 제2 법칙에 대한 사고 실험으로, Maxwell이 (Maxwell 방정식으로 알려진 그 Maxwell이다) 1871년에 출간한 저서 「Theory of Heat」에서 처음 언급된 실험이다. 해당 내용을 Leff & Rex 2002에서 재인용 한 것은 다음과 같다.

(원문) Before I conclude, I wish to direct attention to an aspect of the molecular theory which deserves consideration.

One of the best established facts in thermodynamics is that it is impossible in a system enclosed in an envelope which permits neither change of volume nor passage of heat, and in which both the temperature and the pressure are everywhere the same, to produce any inequality of temperature or of pressure without the expenditure of work. This is the second law of thermodynamics, and it is undoubtedly true as long as we can deal with bodies only in mass, and have no power of perceiving or handling the separate molecules of which they are made up. But if we conceive a being whose faculties are so sharpened that he can follow every molecule in its course, such a being, whose attributes are still as essentially finite as our own, would be able to do what is at present impossible to us. For we have seen that the molecules in a vessel full of air at uniform temperature are moving with velocities by no means uniform, though the mean velocity of any great number of them, arbitrarily selected, is almost exactly uniform. Now let us suppose that such a vessel is divided into two portions, A and B, by a division in which there is a small hole, and that a being, who can see the individual molecules, opens and closes this hole, so as to allow only the swifter molecules to pass from A to B, and only the slower ones to pass from B to A. He will thus, without expenditure of work, raise the temperature of B and lower that of A, in contradiction to the second law of thermodynamics.

This is only one of the instances in which conclusions which we have drawn from our experience of bodies consisting of an immense number of molecules may be found not to be applicable to the more delicate observations and experiments which we may suppose made by one who can perceive and handle the individual molecules which we deal with only in large masses.

In dealing with masses of matter, while we do not perceive the individual molecules, we are compelled to adopt what I have described as the statistical method of calculation, and to abandon the strict dynamical method, in which we follow every motion by the calculus.

아래는 내 국역이다. 대괄호로 묶은 단어는 원문에는 없는 표현으로, 내가 임의로 넣은 단어다.

(국역) 결론 이전에, 분자 [층위] 이론에서 다룰 가치가 있을 법한 한 측면에 대해 거론하고자 한다.

잘 알려진 열역학의 사실 중 하나로 다음이 있다. 닫힌계에서는 부피 변화나 열 교환이 없고, 온도와 압력이 모든 곳에서 균일할 때, 온도나 압력의 [부분적] 차이를 일(work) 소비 없이 만들어 낼 수 없다. 이것이 열역학 제2 법칙이다. 이는 대량의 질량체로만 이루어져, 그 구성 분자에 대해 인지하거나 개별적으로 조작할 수 없는 물체에 대해서라면 의심할 여지 없이 참이다. 하지만 우리가 모든 분자의 흐름을 좇을 수 있을 만큼 유능한 [지적] 존재를 상상해 보면, 그 [지적] 존재는, 그 속성은 우리만큼이나 유한할 그것은, 지금 우리로서는 불가능한 일을 하나 할 수 있다. 앞서 보았듯 공기로 가득 찬, 균일한 온도를 지닌 통 안의 분자는, 각자의 이동 속도는 전혀 균일하지 않을 것이다. 다만 임의로 상당히 많은 분자를 골랐으면 그 경우에는 평균적으로 거의 균일할 것이다. 이제 이 통을 두 부분 A, B로 나누고, 가름 막에 작은 구멍을 하나 냈다고 하자. 그리고 앞서 생각한, 개별 분자를 좇을 수 있는 [지적] 존재가 이 구멍을 여닫을 수 있어, 더 빠른 분자만 A에서 B로 움직이고, 더 느린 분자만 B에서 A로 이동할 수 있다고 하자. 그러면 그 존재는 특별히 일(work)을 소비하지 않고도 B의 온도를 높이고 A의 온도를 낮출 수 있다. 이는 열역학 제2 법칙에다 모순이다.

이는 아주 많은 수의 분자를 갖춘 계에 대해 우리가 실험적으로 알게 된 사실이, (지금 우리로서는 많은 수 단위로밖에 다루지 못하는) 개별 분자를 인지하고 조작할 수 있는 이가 할 수 있을 법한, 좀 더 섬세한 관찰이나 실험에 적용될 수 없는 사례 중 하나일 뿐이다.

많은 수의 물질을 다룰 때는, 비록 우리가 개별 분자를 인지하지는 못하지만, 앞서 저자가 칭한 「통계적 계산」을 도입할 수밖에 없다. 곧 모든 운동을 미적분학으로 추적하는 엄격한 동역학적 기법을 피해야 할 것이다.

흔히 다음과 같은 그림으로 Maxwell이 묘사한 ‘존재’를 묘사하곤 한다.

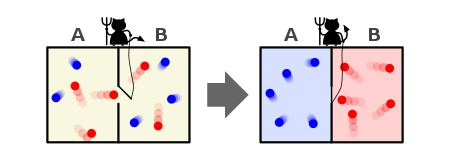
위 그림에서 두 방 A, B 사이에 두 방의 분자를 모두 관찰하는 ‘지적 존재’가 있다고 하자. 그 ‘지적 존재’는 그림에서 출입문으로 보이는, A와 B 사이에 분자가 오고 갈 수 있는 통로를 제어하고 있다. 이 제어권으로 A에서 속도가 빠른 분자가 B로, B에서 속도가 느린 분자가 A로 가도록 유도한다고 생각하자. 이 출입문을 계속 가동함으로써 A와 B에 평균적인 기체 분자 속력을 제어할 수 있다. 기체 분자의 평균속력이 온도에 정비례함은 열역학적으로 잘 알려져, 원문에서는 이를 ‘한쪽은 온도가 높아지고 한쪽은 온도가 낮아진다’라고 묘사하고 있다.

열역학 제2 법칙에 따르면, 애초에 분자들의 평균속력이 전체적으로 균일해졌으면 그러한 채로 있으려 하지, 다시 빠른 분자끼리 혹은 느린 분자끼리 다시 모이려 하지 않는다. (낮은 확률로 우연히 다시 모일 수는 있다. 굉장히 낮은 확률로.) 그런데 이 사고 실험은 적절한 ‘지적 존재’ 내지는 ‘관찰자’를 설치함으로써 열역학 제2 법칙을 우회할 수 있다는 결론을 내고 있으니, Maxwell 입장에서는 짚고 넘어갈 수밖에 없었을 것이다.

위 인용문에서 보이듯 Maxwell은 이것을 통계적 관점과 개별 분자 관점의 차이로 해설했다. 곧, 이 사고 실험은 열역학 제2 법칙이 많은 분자로 이루어진 계에서 벌어지는 통계적 현상임을 다시금 보여주고 있다. 가령, 두 부분으로 나뉜 기체에 작은 구멍을 뚫고 잠시 내버려 두면, 아주 작은 확률로나마 (Maxwell의 ‘지적 존재’처럼) 균일하지 않은 분자 분포를 만들어낼 수 있을 것이다 (Leff & Rex 2002).

영문명 Maxwell’s demon은 W. Thompson의 명명이라 전해진다. Demon은 그리스어 원어로는 ‘초자연적 존재’를 칭하는데, 이것이 시간이 지나면서 ‘악마’라는 번역어를 달게 되어 한 때에는 ‘Maxwell의 악마’로 국역된 것으로 보인다. 그러나 원래 demon이라는 단어 자체가 선악과는 무관하게 - 혹은 단순히 ‘초자연적인’ 단어가 필요해서 – 도입된 만큼, 이 글을 쓰는 지금은 한국어 위키피디아에 ‘Maxwell의 도깨비’로 번역된 것으로 보인다. (혹여나 ‘Maxwell의 괴력난신怪力亂神’이란 칭호도 이런 맥락에서 쓰임직할까 싶었다.)

미시적 Maxwell의 도깨비와 그 해결

물론 Maxwell 본인이 통계적 관점과 개별 분자 관점에서의 차이로 그의 사고 실험을 설명하기는 했다. 여기에 나아가 Maxwell은 열역학 제2 법칙이 통계적으로만 확실한 법칙이라 보고 있었던 모양이다.

그렇다고 해서 Maxwell이 던지고 간 숙제가 단순한 자문자답自問自答으로 끝나지는 않았다. 열역학 제2 법칙이 통계적 관점에서는 참인데, 개별 분자 관점에서도 참일까? 저 멀쩡히 있는 Maxwell의 도깨비는 이 법칙을 (미시적 수준에서) 어디까지 꼬아 놓을까? 등등의 질문이 연이어 남은 것이다.

다만 이하에서 염두에 둘 열역학 제2 법칙은 앞서 통계적 사실로만 언급한 ‘이미 섞인 것은 일(work) 없이 재분류되지 않는다’가 아니라, 미시적으로도 의미가 있는 ‘엔트로피 증가법칙’이다. 가령 Maxwell의 도깨비가 일하고 난 후 분자가 분류된 상태는 엔트로피가 낮아진 상태로, 이 과정이 별 외부 작용 없이 엔트로피가 저절로 낮아지는 것처럼 보이는 것이 ‘Maxwell의 도깨비 문제’의 시작이라 할 수 있다.

이 질문에 대해 크게 두 가지 큰 발견이 있었다.

• Szilard 1929: 분자의 속도 등 상태를 측정하는 과정에서 (대개) 엔트로피가 증가한다.
• Landauer 1961: 측정 과정이 가역적이면 꼭 엔트로피가 증가할 이유는 없다. 그러나 정말 Maxwell의 도깨비가 일하는 과정이 가역적이면 분자를 분류한 후 ‘아무것도 모르는 상태’로 - 즉 메모리 완전 삭제로 - 돌아가야 하는데, 그 과정에서 분자를 분류하며 낮아진 엔트로피를 도로 돌려내야 한다.

이들 답에 대한 자세한 해설은 Leff & Rex 2002에서 찾아 볼 수 있다. 이 ‘Maxwell의 도깨비 퇴치(exorcism of Maxwell’s demon)’ 활동은 열역학과 정보이론 사이의 가교를 놓은 발견으로 알고 있다.

잡상

위의 ‘답’에서 보듯, (미시적) Maxwell의 도깨비 문제는 열역학과 정보이론 사이의 가교를 놓은 문제로, 자세히 들어가면 점차 내가 확실하게 말할 수 있는 내용이 거의 없어진다. 이에, 그저 사견의 나열로 글을 이어가고자 한다.

Szilard 모델

Leff & Rex 2002에서의 요약을 내가 읽은 바로는, Szilard의 논거는 다음과 같다.

분자 1개만 있는 기체가 든 방을 생각하고, 그 방을 같은 부피의 2개 방으로 나눈다고 하자. (이 때 파티션이 기체의 압력만으로 움직일 수 있다고 하자.) 그러면 그 분자의 상태는 정확히 1 비트의 정보를 담고 있을 것이다.

Szilard가 제안한 모델을 따라, 이 정보를 어떻게든 알게 됐다고 하고 이를 유용한 일로 바꾼다고 생각하자. 그러면 외부에서 열을 받아 등온 팽창을 통해 (파티션이 피스톤을 미는 등으로) 일을 하는 과정을 생각할 수 있는데, 이 때 기체의 엔트로피 변화는

로 계산할 수 있다. 정확한 논리인지는 모르나, 이 과정은 (일을 반대로 해서) 가역적인 과정으로 만들 수 있고, 따라서 열원에서 $k_B\log 2$만큼 엔트로피를 감소하는 효과를 가져올 것이다.

따라서 ‘정보를 어떻게든 알게 된’ 것 (즉 ‘측정’) 만으로 열원에서 엔트로피가 감소하는 효과를 가져온 셈이다. 이는 블랙박스로 처리했던 ‘측정’에서 엔트로피가 증가했기에 이 엔트로피 감소를 설명할 수 있다는 이론으로 보인다.

정보 질량

최근에 발표된 Vopson 2019의 질량-에너지-정보 등가원리는 다음과 같은 실험적 검증을 제안하고 있다. 완전히 메모리가 삭제된 1TB 용량의 메모리 장치를 가져와서, 여기에 1TB, 곧 $8\times10^{12}$ 비트의 정보를 저장하면 그만큼 ‘정보질량’이 증가한다는 주장인데, 대략 실온 300K에서 $2.5\times 10^{-25}$ kg 수준의 질량 증가를 (이론적으로) 예상하고 있다. 논문은 여기에 현재 질량 측정의 민감도는 최대 $10^{-9}$ kg 수준이라고 첨언하고 있다.

물리적 참거짓을 떠나, Vopson의 이론적 배경을 짚어보면 Landauer 열에 대한 한 가지 해석을 생각할 수 있다. Vopson에 따르면 1개의 이진 비트 정보에 저장된 ‘정보질량’은 다음과 같다.

이는 해당 비트에 대한 Landauer 열 $Q=k_BT\log 2$를 질량-에너지 등가원리 $E=mc^2$와 엮어서 만든 식이다.

사적으로는 이 Vopson의 ‘정보질량’을 보고, Landauer 열을 ‘정보가 있는 비트에 서려 있는 뭔가’로 해석할 수 있었다. (魂魄 같은 말이 문득 떠오르기도 한다.) 이하 실험적 검증이나, Landauer 본인이 설명한 것을 이해하는 데에 이 관점이 꽤나 도움이 되었다. 나아가 수학적인 함의까지 생각해 보는 데에도 상당한 도움이 되었고.

Landauer 열

짧게 이르자면, Landauer의 원리는 (Laundauer’s principle) 1 (이진) 비트의 정보를 삭제하면서 주변 환경에 최소 $k_B\ln 2$의 엔트로피가 증가한다는 내용이다. Leff & Rex 2002에서는 Szilard의 모델과 연계해서 왜 이러한 숫자가 자연스러운지 소개하고 있다.

온도 $T$에 놓인 1개의 이진 비트의 정보가 삭제될 경우, 외부로 엔트로피를 방출하는 과정은 열 방출로 나타나며, 그 평균열량은 $Q_{\text{열원}}\geq T\Delta S = k_BT\ln 2$로 나타난다. 평균임을 강조한 까닭은, 이 삭제 과정에서 $k_BT\ln 2$보다 작은 열량이 방출될 수도 있고, 큰 열량이 방출될 수 있기 때문이다 (아래의 실험적 검증의 데이터를 보면 이러한 변동성은 항상 나타나는 것으로 보인다). 임의로 이 열을 Landauer 열이라고 부르자. (즉, 이 용어가 표준용어인지는 잘 모른다.)(Vopson의 정보질량 이론은 이를 되려 정보 자체가 가지고 있는 내재된 에너지/질량으로 보는 것으로 이해하고 있다.)

볼츠만 상수가 상당히 작은 상수라 (혹은 아보가드로 상수가 상당히 큰 상수라) $T=300\;\mathrm{K}$만 해도 $2.87\times 10^{-21}\;\mathrm{J}$ 수준의 매우 작은 에너지가 방출되기에, 실험적인 검증이 오랫동안 힘들지 않았을까 싶다. 이 개념은 Landauer가 실제로 제시한 이중 퍼텐셜 우물에 놓인 입자를 가지고 2012년 실험적으로 검증됐다.

Nature에 게재된 Bérut, et al. 2012에서는 콜로이드 입자에 이중 퍼텐셜 우물을 레이저로 구현하고, 메모리 삭제 과정도 이 퍼텐셜 우물을 제어함으로써 관련한 열 방출을 점성력의 적분 형태로 추적하였다. 그 과정에서, 초기 상태에 관계없이 점근적으로 $k_BT\ln 2$만큼의 열 방출을 파악할 수 있었고, 그에 따라 Landauer 열 개념을 검증할 수 있었다.

수학에서는?

이상의 정보 측정과 열 간의 관계를 보고 있으면, 마치 정보가 하나의 물리량처럼 이리저리 교환되는 광경을 보게 된다. 아마 이것이 Maxwell의 도깨비에 얽힌 물리학의 정수겠거니 싶으면서도, 나아가 이런 질문을 생각케 한다.

왜 수학의 동역학 이론에서는 엔트로피를 물리량처럼 다루는 이야기가 없지?

가령 measure-preserving dynamical system $(X,T,\mu)$를 생각하고, 그 measure-theoretic entropy (a.k.a. Kolmogorov-Sinai entropy)를 생각하자. 그 entropy를 알아내는 과정에서 동역학계 $X$ 자체에 뭔가 변화를 주는 등의 영향은 없다. 단지 얼마나 $X$의 partition을 더 refine해야 더 정확한 entropy를 얻겠냐 정도가 동역학계의 그나마의 존재감으로 보인다.

이는 수학에서 동역학계를 분석하는 관점이 철저하게 외부 관찰자 시선이어서 그런 것이 아닐까 싶다. 이 관점에서 동역학계는 고정되어 있고, 그 계를 외부에서 perturb할 방법은 없다. (임의로 $T$를 perturb하는 건 아예 새로운 동역학계를 만드는 작업이다.)

한편 Maxwell의 도깨비에서 나타나는 측정-엔트로피 발생이나 정보-열에너지 교환은 도깨비를 구성하는 물리적 구성체를 생각해 본다면 사실 그리 어색한 개념은 아니다. Maxwell의 도깨비 본체(?)도 애초에 물리계의 일부인 이상, 빛을 쏘건 뭘 하건 분자의 상태를 알아보는 과정에서 본체도 영향을 안 받을 수 없는 것이다. 이런 점에서 볼 때 Maxwell의 도깨비는 물리계 내부의 관찰자고, 그 관찰자가 가져야 하는 여러 물리적인 필연성을 가지는 셈이다.

따라서 비슷한 이론을 수학에서 생각해 보고자 한다면, 동역학계 $(X,T,\mu)$ 내부에서 동역학계를 관찰하는 subsystem을 생각해야 합리적일 것이다. 즉,

수학의 동역학 이론에서 ‘내부 관찰자’를 생각할 수 있을까?

어떻게?는 차차 생각해 볼 문제지만. 아마 factor $(X,T)\to(Y,T’)$가 아닐까 싶기는 하다. 물리계 전체와 컴퓨터의 관계에 빗대어 생각하면, 전체 phase space $X$ 중 컴퓨터와 관련한 phase space $Y$는 $X$의 부분이라기보다는 $X$의 quotient space에 더 가까워 보이기 때문이다. (알파 센타우리에서 5년 전에 생긴 흑점이 내일 내 컴퓨터의 블루스크린 확률을 더 올린다고 생각하면 매우 혼란스럽지 않을까? 그런 영향력을 빼고 생각한다는 점에서 quotienting이라 본 것이다.)

Update Log

• 221216: Created
• 221220: Landauer 열 관련 오개념 정정